辽宁省建平县2012年八年级数学竞赛试卷
试卷更新日期:2018-03-23 类型:竞赛测试
一、单选题
-
1. 直角三角形的周长为12cm,斜边长为5cm,则其面积为( )A、12cm2 B、6cm2 C、8cm2 D、10cm22. 在△ABC中,∠A、∠B、∠C的对边分别是 、 、 ,则下列说法中错误的是( )A、如果∠C-∠B=∠A,那么△ABC是直角三角形,∠C=90° B、如果 ,则∠B=60°,∠A=30° C、如果 ,那么△ABC是直角三角= D、如果 ,那么△ABC是直角三角形3. 已知x2+kxy+64y2是一个完全平方式,则k的值是( )A、8 B、±8 C、16 D、±164. 若A(a,b),B(b,a)表示同一点,那么这一点在 ( )
A、第一、三象限内两坐标轴夹角平分线上 B、第一象限内两坐标轴夹角平分线上 C、第二、四象限内两坐标轴夹角平分线上 D、平行于y轴的直线上5. 已知 是整数,则x的最小整数值是( )
A、16 B、±16 C、25 D、±256. 下列说法,正确的是( )A、在△ABC中, ,则有 B、0.125的立方根是±0.5 C、无限小数是无理数,无理数也是无限小数 D、一个无理数和一个有理数之积为无理数7. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽《勾股圆方图》,它是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,如图,如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为 ,较长直角边为 ,那么 的值为( )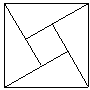 A、13 B、36 C、25 D、1698. 若0< <1,那么 的化简结果是( )
A、13 B、36 C、25 D、1698. 若0< <1,那么 的化简结果是( )
A、 B、 C、 D、二、填空题
-
9. 已知a+b=1,ab=108,则a2b+ab2的值为 .
10. 如图,长方体中,AB=12cm,BC=2cm,B =3cm,一只蚂蚁从点A出发,以4cm/秒的速度沿长方体表面爬行到点 ′ , 至少需要分钟.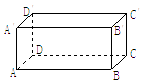 11. 如图,AD=8cm,CD=6cm,AD⊥CD,BC=24cm,AB=26cm,则S四边形ABCD=.
11. 如图,AD=8cm,CD=6cm,AD⊥CD,BC=24cm,AB=26cm,则S四边形ABCD=.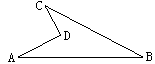 12. 如图,要在高3m,斜坡5m的楼梯表面铺地毯,地毯的长度至少需 _m.
12. 如图,要在高3m,斜坡5m的楼梯表面铺地毯,地毯的长度至少需 _m.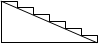
 13. 任意找一个小于1的正数,利用计算器对它不断进行开立方运算,其结果如何?根据这一规律,则 a(0<a<1).(填“>”、“<”、“≤”、“≥”)14. 若 与 是同一个数的平方根,则 的值为.15. 已知3 =3,3 =9,3 =27,3 =81,3 =243,3 =729, 37=2187,3 =6561……,请你推测3 的个位数是.
13. 任意找一个小于1的正数,利用计算器对它不断进行开立方运算,其结果如何?根据这一规律,则 a(0<a<1).(填“>”、“<”、“≤”、“≥”)14. 若 与 是同一个数的平方根,则 的值为.15. 已知3 =3,3 =9,3 =27,3 =81,3 =243,3 =729, 37=2187,3 =6561……,请你推测3 的个位数是.
16. 已知a1+a2=1,a2+a3=2,a3+a4=3,…,a99+a100=99,a100+a1=100,那么a1+a2+a3+…a100= 。
三、解答题
-
17. 化简:
(1)、 ;(2)、18. 已知 的和仍为单项式,求多项式 的值.
19. 如果 ,试求代数式 的值.20. “震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.(1)、求打包成件的帐篷和食品各多少件?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.(3)、在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?21. 一个零件的形状如图所示,按规定∠A应等于1200 , ∠B、∠D应分别为150、200.李叔叔量得∠BCD=1450 , 就能断定该零件不合格,你能说出其中的道理吗? 22. 国庆60周年阅兵式上,向世界展示了一种新型导弹―“红-九地空导弹”.它是我国自行研制的远程防空导弹,集美俄技术于一身,以拦截飞机为主,同时具有很强的拦截短程弹道导弹的能力.10枚“红-九地空导弹”(每枚底面的直径均为0.4m)以如图方式堆放,为了防雨,需要搭建防雨棚,这个防雨棚的最低高度应为多少米(精确到0.1m)?
22. 国庆60周年阅兵式上,向世界展示了一种新型导弹―“红-九地空导弹”.它是我国自行研制的远程防空导弹,集美俄技术于一身,以拦截飞机为主,同时具有很强的拦截短程弹道导弹的能力.10枚“红-九地空导弹”(每枚底面的直径均为0.4m)以如图方式堆放,为了防雨,需要搭建防雨棚,这个防雨棚的最低高度应为多少米(精确到0.1m)? 23. 任画一个直角三角形,分别以它的三条边为边向外做等边三角形,
23. 任画一个直角三角形,分别以它的三条边为边向外做等边三角形,要求:
(1)、画出图形;(2)、探究这三个等边三角形面积之间的关系,并说明理由.24. 国际象棋中的“皇后”不仅能控制她所在的行与列的每一个小方格,而且还能控制“斜”方向的两条直线上的每个小方格,如图甲所示.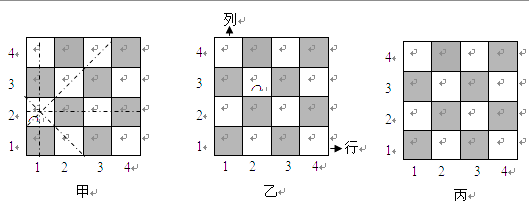 (1)、在图乙小方格中有一“皇后Q”他所在的位置可用(2,3)来表示,请说明“皇后Q”所在的位置(2,3)的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置;(2)、图丙是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间胡不受对方控制.(在图丙中标出字母Q即可)
(1)、在图乙小方格中有一“皇后Q”他所在的位置可用(2,3)来表示,请说明“皇后Q”所在的位置(2,3)的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置;(2)、图丙是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间胡不受对方控制.(在图丙中标出字母Q即可)
25. 某粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较高安全系数A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表(表中“元/吨·千米”表示每吨粮食运送1千米所需人民币) (1)、若甲库运往A库粮食
(1)、若甲库运往A库粮食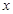 吨,请写出将粮食运往A、B两库的总运费
吨,请写出将粮食运往A、B两库的总运费 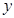 (元)与
(元)与 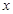 (吨)的函数关系式;
(吨)的函数关系式;
(2)、当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?26. 如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得他们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合.(在图3至图6中统一用F表示)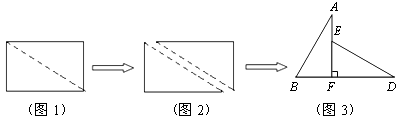
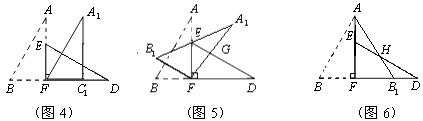
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)、将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;(2)、将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;(3)、将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请说明:AH=DH.