辽宁省建平县2011年八年级数学竞赛试卷
试卷更新日期:2018-03-23 类型:竞赛测试
一、单选题
-
1. 下列多项式能用完全平方公式分解的是( )
A、x2-2x- B、(a+b) (a-b)-4ab C、a2+ab+ D、y2+2y-12. 根据下列表述,能确定位置的是( )A、某电影院2排 B、南京市大桥南路 C、北偏东30° D、东经118°,北纬40°3. 有19位同学参加歌咏比赛,所得的分数互不相同,取得分排前10位的同学进入决赛.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学成绩的( )
A、平均数 B、中位数 C、众数 D、加权平均数4.以下五家银行行标中,既是中心对称图形又是轴对称图形的有( )




 A、1个 B、2个 C、3个 D、4个5. 若正比例函数的图象经过点(-1,2),则这个图像必经过点( )
A、1个 B、2个 C、3个 D、4个5. 若正比例函数的图象经过点(-1,2),则这个图像必经过点( )
A、(1,2) B、(-1,-2) C、(2,-1) D、(1,-2)6. 如图,小手盖住的点的坐标可能为( ) A、(5,2) B、(-6,3) C、(-4,-6) D、(3,-4)7. 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△APB的面积S与点P运动的路程之间的函数图象大致是( )
A、(5,2) B、(-6,3) C、(-4,-6) D、(3,-4)7. 如图,在矩形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D作匀速运动,那么△APB的面积S与点P运动的路程之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则下列函数关系中正确的是( )
8. 图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则下列函数关系中正确的是( )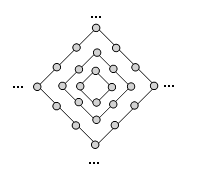 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 写出一个解为 的二元一次方程组是10. 的平方根是 , 算术平方根是.
11. 已知x+y=1,则 = .
12. 当x=1时,分式 无意义,当x=4分式的值为零, 则 =_.13. 在直线l上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个正方形的面积依次是S1 , S2 , S3 , S4 , 则S1 + S2 +S3 +S4 = . 14. 已知, 用 的代数式表示 ,则 .
14. 已知, 用 的代数式表示 ,则 .
15. 如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,拆痕为EF , 则重叠部分△DEF的边ED的长是 . 16. 函数 与 的图象如图所示,这两个函数的图象交点在y轴上,则使得 的值都大于零的x的取值范围是.
16. 函数 与 的图象如图所示,这两个函数的图象交点在y轴上,则使得 的值都大于零的x的取值范围是.
三、解答题
-
17. 综合题
(1)、解不等式组 并将其解集在数轴上表示出来。(2)、当 时,求 - ÷ 的值.
18. 已知:方程组, 求:x2-y2的值。
19. 综合题
(1)、如图所示,经过平移,△ABC的顶点B移到了点E,作出平移后的三角形。 (2)、用图象的方法解方程组
(2)、用图象的方法解方程组 20. 如图,若∠AOB=∠ACB=90°,OC平分∠AOB.
20. 如图,若∠AOB=∠ACB=90°,OC平分∠AOB. (1)、你能将四边形AOBC通过剪裁拼成一个正方形吗?画出裁剪方法并有必要的说明。(2)、若OC=2,你能求出四边形AOBC的面积吗?21. 阅读:①方程 x+ =2+ 的解为:x1=2;x2=
(1)、你能将四边形AOBC通过剪裁拼成一个正方形吗?画出裁剪方法并有必要的说明。(2)、若OC=2,你能求出四边形AOBC的面积吗?21. 阅读:①方程 x+ =2+ 的解为:x1=2;x2=②方程x+ =m+ 的解为:x1=m;x2=
③方程x- =m- 的解为:x1=m;x2= -
归纳:④方程 x+ =b+ 的解为:x1= b ;x2=
应用:⑤利用④中的结论,直接解关于x的方程:x+ =a+
22. 为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了10名同学参加决赛(满分为100分)如表所示:决赛成绩(单位:分)
 (1)、请你填写下表:
(1)、请你填写下表:平均数
众数
中位数
七年级
85.5
87
八年级
85.5
85
九年级
84
(2)、请从以下两个不同的角度对三个年级的决赛成绩进行分析:从平均数和众数相结合看(分析哪个年级成绩好些):;
从平均数和中位数相结合看(分析哪个年级成绩好些):;
(3)、如果在每个年级参加决赛的选手中分别选出三人参加决赛,你认为哪个年级的实力更强一些。说明理由:。
23. 甲、乙两地相距135千米,大小两辆汽车从甲地开往乙地,大汽车比小汽车早出发4小时,小汽车比大汽车早到30分钟,小汽车和大汽车的速度之比为5∶2,求两车的速度.
24. 在四边形ABCD中,对角线相交于点O;E、F、G、H分别是AD、BD、 BC、AC的中点. (1)、说明四边形EFGH是平行四边形;(2)、当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并说明理由.25. 某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李票y(元)与行李质量x(千克)间的一次函数关系式为y=kx-5(k≠0),现知贝贝带了60千克的行李,交了行李费5元。
(1)、说明四边形EFGH是平行四边形;(2)、当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并说明理由.25. 某长途汽车站规定,乘客可以免费携带一定质量的行李,若超过该质量则需购买行李票,且行李票y(元)与行李质量x(千克)间的一次函数关系式为y=kx-5(k≠0),现知贝贝带了60千克的行李,交了行李费5元。
(1)、若京京带了84千克的行李,则该交行李费多少元?
(2)、旅客最多可免费携带多少千克的行李?
26. 某游泳馆的游泳池长50米,甲、乙二人分别在游泳池相对的A、B两边同时向另一边游去,其中s表示与A边的距离,t表示游泳时间,如图,l1 , l2分别表示甲、乙两人的s与t的关系. (1)、l1表示谁到A边的距离s与游泳时间t的关系;(2)、甲、乙哪个速度快?(3)、游泳多长时间,两人相遇?(4)、t=30秒时,两人相距多少米?
(1)、l1表示谁到A边的距离s与游泳时间t的关系;(2)、甲、乙哪个速度快?(3)、游泳多长时间,两人相遇?(4)、t=30秒时,两人相距多少米?