安徽省芜湖市南陵县许镇镇2016-2017学年七年级下学期数学竞赛试卷

试卷更新日期：2018-03-23 类型：竞赛测试

进入出卷网下载

一、单选题

1. 若 $- 1 < a < 0$ ，则a , $\frac{1}{a}$ ， $a^{2}$ 从小到大排列正确的是（）

A、 $a^{2} < a < \frac{1}{a}$ B、 $a < \frac{1}{a} < a^{2}$ C、 $\frac{1}{a} < a < a^{2}$ D、 $a < a^{2} < \frac{1}{a}$

查看试题解析
2. 下列运用等式的性质，变形不正确的是（）

A、若x=y，则x+5=y+5 B、若a=b，则ac=bc C、若 $\frac{a}{c}$ = $\frac{b}{c}$ ，则a=b D、若x=y，则 $\frac{x}{a} = \frac{y}{a}$

查看试题解析
3. 已知有理数a，b在数轴上对应的两点分别是A，B．请你将具体数值代入a，b，实验验证：对于任意有理数a，b，计算A，B两点之间的距离正确的公式一定是（）

A、b﹣a B、|b|+|a| C、|b|﹣|a| D、|b﹣a|

查看试题解析
4. 若A和B都是3次多项式，则A+B一定是（）

A、6次多项式 B、3次多项式 C、次数不高于3次的多项式 D、次数不低于3次的多项式

查看试题解析
5. 一个多项式与x²-2x+1的和是3x-2，则这个多项式为（）

A、x²-5x+3 B、-x²+x-1 C、-x²+5x-3 D、x²-5x-13

查看试题解析
6. 若 $2 y^{2} + 3 y + 7$ 的值为8，则 $4 y^{2} + 6 y - 9$ 的值是（）．

A、2 B、-17 C、-7 D、7

查看试题解析
7. 一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所示，则被截去部分纸环的个数可能是（）

A、2010 B、2011 C、2012 D、2013

查看试题解析
8. 六个整数的积 $a \cdot b \cdot c \cdot d \cdot e \cdot f = - 36$ ， $a 、 b 、 c 、 d 、 e 、 f$ 互不相等，则 $a + b + c + d + e + f$ 的和可能是（）.

A、0 B、10 C、6 D、8

查看试题解析
9. 把100个苹果分给若干个小朋友，每个人至少一个，且每个人分的数目不同．那么最多有（）人？

A、11 B、12 C、13 D、14

查看试题解析
10. 方程 $\frac{x}{3} + \frac{x}{15} + \frac{x}{35} + ... + \frac{x}{2005 \times 2007} = 1$ 的解是 $x$ 等于（）

A、 $\frac{2006}{2007}$ B、 $\frac{2007}{2006}$ C、 $\frac{2007}{1003}$ D、 $\frac{1003}{2007}$

查看试题解析

二、填空题

11. 如果 $a \cdot b$ ＜0，那么 $\frac{| a |}{a} + \frac{b}{| b |} + \frac{| a b |}{a b}$ = ．

查看试题解析
12. 如果 $(a + 4) x^{| a + 3 |} + 8 = 0$ 是关于x的一元一次方程，那么 $a^{2} + a - 1 =$ ．

查看试题解析
13. 在图中每个小方格内填入一个数，使每一行、每一列都有1、2、3、4、5．那么，右下角的小方格（用粗线围出的方格）内填入的数应是．

查看试题解析
14. 如上图，一个正方体的每个面分别标有数字1，2，3，4，5，6．根据图中该正方体三种状态所显示的数据，可推出“？”处的数字是.

查看试题解析
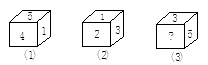15. 将一张长方形的纸对折，如图所示可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得到7条折痕，那么对折10次可以得到条折痕．

查看试题解析
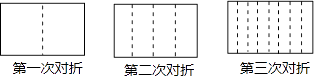16. 已知AB是一段只有3米长的窄道路，由于一辆小汽车与一辆大卡车在AB段相遇，必须倒车才能继续通过．如果小汽车在AB段正常行驶需10分钟，大卡车在AB段正常行驶需20分钟，小汽车在AB段倒车的速度是它正常行驶速度的 $\frac{1}{5}$ ，大卡车在AB段倒车的速度是它正常行驶的 $\frac{1}{8}$ ，小汽车需倒车的路程是大卡车的4倍．问两车都通过AB这段狭窄路面的最短时间是分钟．

查看试题解析
17. 图为手的示意图，在各个手指间标记字母 A，B，C，D.请你按图中箭头所指方向（即 A→B→C→D→C→B→A→B→C → … 的方式）从 A 开始数连续的正整数 1，2，3，4，…，当数到 $12$ 时，对应的字母是；当字母C第 $201$ 次出现时，恰好数到的数是；当字母C第 $2 n + 1$ 次出现时（ $n$ 为正整数），恰好数到的数是（用含 $n$ 的代数式表示）.

查看试题解析
18. 如图，是用棋子摆成的图案，摆第1个图案需要7枚棋子，摆第2个图案需要19枚棋子，摆第3个图案需要37枚棋子，按照这样的方式摆下去，则摆第6个图案需要枚棋子，摆第n个图案需要枚棋子．

查看试题解析
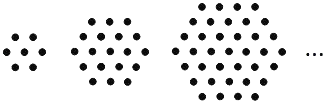19. 扑克牌游戏：小明背对小亮，让小亮按下列四个步骤操作：
第一步，分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；
第二步，从左边一堆拿出两张，放入中间一堆；
第三步，从右边一堆拿出一张，放入中间一堆；
第四步，左边一堆有几张牌，就从中间一堆拿出几张牌放入左边一堆.
这时，小明准确地说出了中间一堆牌现有的张数，聪明的你，你认为中间一堆牌的张数是多少？

查看试题解析

三、解答题

20. 计算题

(1)、计算： $\frac{- 5^{3} - （ - 1 ）^{100} - 12 \div （ - \frac{1}{2^{2}} ）}{1 + | - 1 - 3^{2} \times 2 |}$

(2)、解方程： $\frac{1}{2} {\frac{1}{2} [\frac{1}{2} (\frac{1}{2} x - 3) - 3] - 3} - 3 = 0$

查看试题解析
21. 如果有理数a，b满足 $| a b - 2 | + {(1 - b)}^{2} = 0$ ，试求 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)} + \frac{1}{(a + 2) (b + 2)} + \cdot \cdot \cdot + \frac{1}{(a + 2007) (b + 2007)}$ 的值。

查看试题解析
22. 已知有理数 $a 、 b 、 c$ 在数轴上的位置如图，化简： $| a | - | a + b | + | c - a | + | b + c |$

查看试题解析
23. 已知：a为有理数， $a^{3} + a^{2} + a + 1 = 0$ ，求 $1 {+a+a}^{2} {+a}^{3} {+a}^{4} + \dots {+a}^{2012}$ 的值．

查看试题解析
24. 已知某一铁路桥长1000米，现有一列火车从桥上通过，小亮和小芳从不同的角度进行了观察：小亮：火车从开始上桥到完全通过共用1分钟．小芳：整个火车完全在桥上的时间为40秒钟．请根据以上信息，求出火车的长度和火车的速度．

查看试题解析
25. 已知在数轴l上，一动点Q从原点O出发，沿直线l以每秒钟2个单位长度的速度来回移动，其移动方式是先向右移动1个单位长度，再向左移动2个单位长度，又向右移动3个单位长度，再向左移动4个单位长度，又向右移动5个单位长度…

(1)、求出5秒钟后动点Q所处的位置；

(2)、如果在数轴l上还有一个定点A，且A与原点O相距20个单位长度，问：动点Q从原点出发，可能与点A重合吗？若能，则第一次与点A重合需多长时间？若不能，请说明理由．

查看试题解析
26. 列方程解应用题：由甲地到乙地前三分之二的路是高速公路，后三分之一的路是普通公路，高速公路和普通公路交界处是丙地．A车在高速公路和普通公路的行驶速度都是80千米/时；B车在高速公路上的行驶速度是100千米/时，在普通公路上的行驶速度是70千米/时，A，B两车分别从甲、乙两地同时出发相向行驶，在高速公路上距离丙地40千米处相遇，求甲、乙两地之间的距离是多少？

查看试题解析
27. 某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的 $\frac{1}{2}$ 倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价－进价）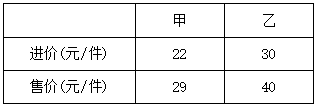

(1)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?

(2)、该超市第二次以第一次的进价又购进甲、乙两种商品．其中甲种商品的件数不变，乙种商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售．第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙种商品是按原价打几折销售？

查看试题解析