备考2018年中考数学一轮基础复习:专题十一 点的坐标、函数及其概念
试卷更新日期:2018-03-21 类型:一轮复习
一、单选题
-
1. 若点P在第二象限内,点P到x轴的距离是5,到y轴的距离是2,则点P的坐标为( )
A、 B、 C、 D、2. 在平面直角坐标系中,点 关于原点的对称点 的坐标是( )A、 B、 C、 D、3. 点P(﹣2,﹣3)向左平移m个单位长度,再向上平移n个单位长度所得对应点Q(﹣3,0),则m+n的值为( )
A、3 B、4 C、5 D、64. 已知点P(x+3,x﹣4)在x轴上,则x的值为( )A、3 B、﹣3 C、﹣4 D、45. 如图,一个点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)→(0,1)→(1,1)→(1,0)→…],那么第35秒时质点所在位置的坐标是( ) A、(4,0) B、(0,5) C、(5,0) D、(5,5)6. 已知点 A(﹣1,1),B(1,1),C(2,4)在同一个函数图象上,这个函数图象可能是( )A、
A、(4,0) B、(0,5) C、(5,0) D、(5,5)6. 已知点 A(﹣1,1),B(1,1),C(2,4)在同一个函数图象上,这个函数图象可能是( )A、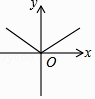 B、
B、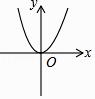 C、
C、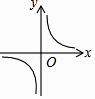 D、
D、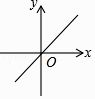 7. 如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(﹣1,1),(﹣3,1),(﹣1,﹣1),30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
7. 如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(﹣1,1),(﹣3,1),(﹣1,﹣1),30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )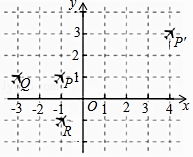 A、Q′(2,3),R′(4,1) B、Q′(2,3),R′(2,1) C、Q′(2,2),R′(4,1) D、Q′(3,3),R′(3,1)8. 如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )
A、Q′(2,3),R′(4,1) B、Q′(2,3),R′(2,1) C、Q′(2,2),R′(4,1) D、Q′(3,3),R′(3,1)8. 如图,点A在观测点北偏东30°方向,且与观测点的距离为8千米,将点A的位置记作A(8,30°).用同样的方法将点B,点C的位置分别记作B(8,60°),C(4,60°),则观测点的位置应在( )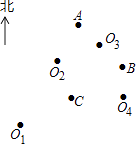 A、点O1 B、点O2 C、点O3 D、点O49. 点P是图①中三角形上一点,坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P′的坐标为( )
A、点O1 B、点O2 C、点O3 D、点O49. 点P是图①中三角形上一点,坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P′的坐标为( )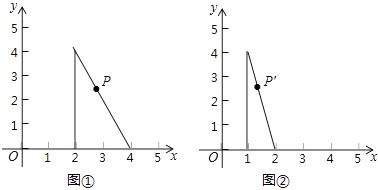 A、( a,b) B、(a﹣1,b) C、(a﹣2,b) D、( a, b)10. 若点A(a+1,b﹣1)在第二象限,则点B(﹣a,b+2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 下列曲线中不能表示y与x的函数的是( )A、
A、( a,b) B、(a﹣1,b) C、(a﹣2,b) D、( a, b)10. 若点A(a+1,b﹣1)在第二象限,则点B(﹣a,b+2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 下列曲线中不能表示y与x的函数的是( )A、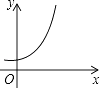 B、
B、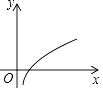 C、
C、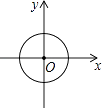 D、
D、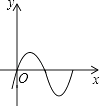 12. 如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( )
12. 如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( ) A、(1,3) B、(3,﹣1) C、(﹣1,﹣3) D、(﹣3,1)13.
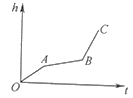
A、(1,3) B、(3,﹣1) C、(﹣1,﹣3) D、(﹣3,1)13.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
 A、
A、 B、
B、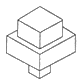 C、
C、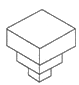 D、
D、 14. 在平面直角坐标系中,点A的坐标为(﹣1,2),点B的坐标为(5,4),则线段AB的中点坐标为( )A、(2,3) B、(2,2.5) C、(3,3) D、(3,2.5)15. 无论m为何值,点A(m,5﹣2m)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
14. 在平面直角坐标系中,点A的坐标为(﹣1,2),点B的坐标为(5,4),则线段AB的中点坐标为( )A、(2,3) B、(2,2.5) C、(3,3) D、(3,2.5)15. 无论m为何值,点A(m,5﹣2m)不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
16. 点P(2-a,a+1)在y轴上,则a=。
17. 在函数y= 中,自变量x的取值范围是 .18. 已知点P的坐标为(5,a),且点P在一、三象限角平分线上,则a= .19. 已知直线a平行于x轴,点M(﹣2,﹣3)是直线a上的一个点,若点N也是直线a上的一个点,请写出符合条件的一个点N的坐标,N( , ).20. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
⑴f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
⑵g(m,n)=(﹣m,﹣n),如g(2,1)=(﹣2,﹣1).
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(2,﹣3)]= .
21. 从1、﹣1、0三个数中任取两个不同的数作为点的坐标,则该点在坐标轴上的概率是 .三、综合题
-
22.
如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1 .
 (1)、在图中画出△A1B1C1;(2)、点A1 , B1 , C1的坐标分别为、、;(3)、若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.23. 在平面直角坐标系中已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,求点P的坐标.24.
(1)、在图中画出△A1B1C1;(2)、点A1 , B1 , C1的坐标分别为、、;(3)、若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.23. 在平面直角坐标系中已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,求点P的坐标.24.已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)
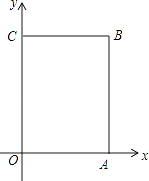 (1)、写出B点的坐标();(2)、当点P移动了4秒时,在图中平面直角坐标系中描出此时P点的位置,并求出点P的坐标;(3)、在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间t.25. 在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.根据所给定义解决下列问题:(1)、若已知点D(1,2)、E(﹣2,1)、F(0,6),则这3点的“矩面积”= .(2)、若D(1,2)、E(﹣2,1)、F(0,t)三点的“矩面积”为18,求点F的坐标.
(1)、写出B点的坐标();(2)、当点P移动了4秒时,在图中平面直角坐标系中描出此时P点的位置,并求出点P的坐标;(3)、在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间t.25. 在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.根据所给定义解决下列问题:(1)、若已知点D(1,2)、E(﹣2,1)、F(0,6),则这3点的“矩面积”= .(2)、若D(1,2)、E(﹣2,1)、F(0,t)三点的“矩面积”为18,求点F的坐标.