备考2018年中考数学一轮基础复习:专题十 一元一次不等式(组)
试卷更新日期:2018-03-21 类型:一轮复习
一、单选题
-
1. 下列给出四个式子,①x>2;②a≠0;③5<3;④a≥b,其中是不等式的是( )A、①④ B、①②④ C、①③④ D、①②③④2. 已知不等式组 的整数解有三个,则a的取值范围是( )A、1<a≤2 B、2≤a<3 C、1<a<2 D、1≤a<23. 若干个苹果分给x个小孩,如果每人分3个,那么余7个;如果每人分5个,那么最后一人分到的苹果不足5个,则x满足的不等式组为( )A、0<(3x+7)﹣5(x﹣1)≤5 B、0<(3x+7)﹣5(x﹣1)<5 C、0≤(3x+7)﹣5(x﹣1)<5 D、0≤(3x+7)﹣5(x﹣1)≤54. 如图为一隧道入口处的指示标志牌,图①表示汽车的高度不能超过3.5 m,
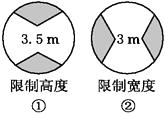
由此可知图②表示汽车的宽度l(m)应满足的关系为( )
A、l≥3 B、l>3.5 C、l≤3 D、l≥3.55. 已知x>y,若对任意实数a,以下结论:甲:ax>ay;乙:a2﹣x>a2﹣y;丙:a2+x≤a2+y;丁:a2x≥a2y
其中正确的是( )
A、甲 B、乙 C、丙 D、丁6. 已知实数a,b满足a+1>b+1,则下列选项错误的为( )A、a>b B、a+2>b+2 C、﹣a<﹣b D、2a>3b7. 若关于x的不等式x﹣ <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定8. 不等式6﹣4x≥3x﹣8的非负整数解为( )A、2个 B、3个 C、4个 D、5个9. 关于x的一元一次不等式 ≤﹣2的解集为x≥4,则m的值为( )A、14 B、7 C、﹣2 D、210.如图天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围在数轴上可表示为( )
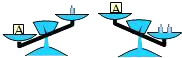 A、
A、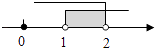 B、
B、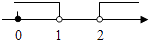 C、
C、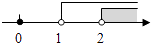 D、
D、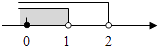 11. 如果点P(2 x +6,x -4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )A、
11. 如果点P(2 x +6,x -4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )A、 B、
B、 C、
C、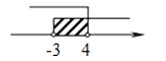 D、
D、 12. 现有一段旧围墙长20 m,李叔叔想紧靠这段围墙圈一块长方形空地作为兔舍饲养小兔.已知他圈好的空地如图所示,是一个长方形,它的一条边用墙代替,另三边用总长度为50 m的篱笆围成.设垂直于墙的一边的长度为a m,则a的取值范围是( )
12. 现有一段旧围墙长20 m,李叔叔想紧靠这段围墙圈一块长方形空地作为兔舍饲养小兔.已知他圈好的空地如图所示,是一个长方形,它的一条边用墙代替,另三边用总长度为50 m的篱笆围成.设垂直于墙的一边的长度为a m,则a的取值范围是( ) A、20<a<50 B、15≤a<25 C、20≤a<25 D、15≤a≤2013. 如图为某餐厅的价目表,今日每份餐点价格均为价目表价格的九折.若李心通同学在此餐厅点了橙汁鸡丁饭后想再点第二份餐点,且两份餐点的总花费不超过20元,则他的第二份餐点最多有几种选择( )
A、20<a<50 B、15≤a<25 C、20≤a<25 D、15≤a≤2013. 如图为某餐厅的价目表,今日每份餐点价格均为价目表价格的九折.若李心通同学在此餐厅点了橙汁鸡丁饭后想再点第二份餐点,且两份餐点的总花费不超过20元,则他的第二份餐点最多有几种选择( )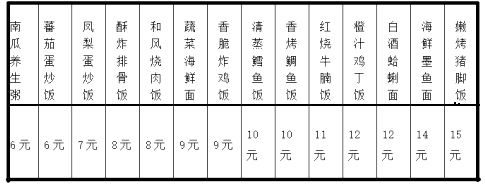 A、5 B、7 C、9 D、1114. 某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至少要答对( )道题.A、12 B、13 C、14 D、1515. 为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买( )A、16个 B、17个 C、33个 D、34个
A、5 B、7 C、9 D、1114. 某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过95分,他至少要答对( )道题.A、12 B、13 C、14 D、1515. 为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买( )A、16个 B、17个 C、33个 D、34个二、填空题
-
16. 如果5a﹣3x2+a>1是关于x的一元一次不等式,则其解集为17. 已知“x的3倍大于5,且x的一半与1的差不大于2”,则x的取值范围是 .18. 运行程序如图所示,从“输入实数x”到“结果是否<18”为一次程序操作,

若输入x后程序操作仅进行了一次就停止,则x的取值范围是 .
19. 有七张正面分别标有数字﹣1、﹣2、0、1、2、3、4的卡片,除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程 + =2的解为正数,且不等式组 无解的概率是 .三、计算题
-
20. 解不等式组 ,把不等式组的解集在数轴上表示出来,并求出不等式组的整数解的和.21. 先化简,再求值:(x﹣1+ )÷ ,其中x的值从不等式组 的整数解中选取.
四、综合题
-
22. 根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
若a﹣b>0,则a>b;若a﹣b=0,则a=b;若a﹣b<0,则a<b.反之也成立.这种比较大小的方法称为“求差法比较大小”.请运用这种方法尝试解决下面的问题:
(1)、比较4+3a2﹣2b+b2与3a2﹣2b+1的大小;(2)、若2a+2b﹣1>3a+b,则a、b的大小关系(直接写出答案).23. 天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?