备考2018年中考数学一轮基础复习：专题九分式方程

试卷更新日期：2018-03-21 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列式子是分式方程的是（）

A、 $\frac{x^{2} + 1}{2} = \frac{5}{3}$ B、 $\frac{1}{3 x - 1} + \frac{4 x}{3 x + 1}$ C、 $\frac{x}{2 x - 1} - \frac{3}{2 x + 1} = 1$ D、 $\frac{3 - x}{4} + 2 = \frac{x - 4}{3}$

查看试题解析
2. 解分式方程 $\frac{1}{x - 1}$ ﹣2= $\frac{3}{1 - x}$ ，去分母得（）

A、1﹣2（x﹣1）=﹣3 B、1﹣2（x﹣1）=3 C、1﹣2x﹣2=﹣3 D、1﹣2x+2=3

查看试题解析
3. 解分式方程 $\frac{2}{x + 1} + \frac{3}{x - 1} = \frac{6}{x^{2} - 1}$ ，分以下四步，其中，错误的一步是（）

A、方程两边分式的最简公分母是（x﹣1）（x+1） B、方程两边都乘以（x﹣1）（x+1），得整式方程2（x﹣1）+3（x+1）=6 C、解这个整式方程，得x=1 D、原方程的解为x=1

查看试题解析
4. 分式方程 $\frac{3}{x + 5}$ ﹣ $\frac{1}{x - 1}$ =0解的情况是（）

A、有解，x=1 B、有解，x=5 C、有解，x=4 D、无解

查看试题解析
5. 分式方程 $\frac{x}{x - 1}$ ﹣1= $\frac{3}{(x - 1) (x + 2)}$ 的解为（）

A、x=1 B、x=﹣1 C、无解 D、x=﹣2

查看试题解析
6. 下列关于分式方程增根的说法正确的是（）

A、使所有的分母的值都为零的解是增根 B、分式方程的解为零就是增根 C、使分子的值为零的解就是增根 D、使最简公分母的值为零的解是增根

查看试题解析
7. 关于x的分式方程 $\frac{7 x}{x - 1}$ +5= $\frac{2 m - 1}{x - 1}$ 有增根，则m的值为（）

A、1 B、3 C、4 D、5

查看试题解析
8. 下列说法中正确的说法有（）
（1）解分式方程一定会产生增根；（2）方程 $\frac{x - 2}{x^{2} - 4 x + 4}$ =0的根为x=2；（3）x+ $\frac{1}{x - 1}$ =1+ $\frac{1}{x - 1}$ 是分式方程．

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 若关于x的方程x+ $\frac{2}{x}$ =c+ $\frac{2}{c}$ 的两个解是x=c，x= $\frac{2}{c}$ ，则关于x的方程的x+ $\frac{2}{x - 1}$ =a+ $\frac{2}{a - 1}$ 的解是（）

A、a， $\frac{2}{a}$ B、a﹣1， $\frac{2}{a - 1}$ C、a， $\frac{2}{a - 1}$ D、a， $\frac{a + 1}{a - 1}$

查看试题解析
10. 某市从今年1月1日起调整居民用水价格，每立方米水费上涨 $\frac{1}{3}$ ．小丽家去年12月份的水费是15元，而今年5月的水费则是30元．已知小丽家今年5月的用水量比去年12月的用水量多5cm³ ．求该市今年居民用水的价格．设去年居民用水价格为x元/cm³ ，根据题意列方程，正确的是（）

A、 $\frac{30}{(1 + \frac{1}{3}) x} - \frac{15}{x} = 5$ B、 $\frac{30}{(1 - \frac{1}{3}) x} - \frac{15}{x} = 5$ C、 $\frac{30}{x} - \frac{15}{(1 + \frac{1}{3}) x} = 5$ D、 $\frac{30}{x} - \frac{15}{(1 - \frac{1}{3}) x} = 5$

查看试题解析
11. 火车提速后，从盐城到南京的火车运行速度提高了25%，运行时间缩短了1h．已知盐城到南京的铁路全长约460km．设火车原来的速度为xkm/h，则下面所列方程正确的是（）

A、 $\frac{460}{x}$ ﹣ $\frac{460}{25 %}$ =1 B、 $\frac{460}{(1 - 25 %) x}$ ﹣ $\frac{460}{x}$ =1 C、 $\frac{460}{x}$ ﹣ $\frac{460}{(1 + 25 %) x}$ =1 D、 $\frac{460}{25 % x}$ ﹣ $\frac{460}{x}$ =1

查看试题解析
12. 一艘轮船在静水中的最大航速为30千米/时，它沿江以最大航速顺流航行100千米所用时间，与以最大航速逆流航行60千米所用时间相等，江水的流速为多少？设江水的流速为 $x$ 千米/时，则可列方程（）

A、 $\frac{100}{30 + x} = \frac{60}{30 - x}$ B、 $\frac{100}{x + 30} = \frac{60}{x - 30}$ C、 $\frac{100}{30 - x} = \frac{60}{30 + x}$ D、 $\frac{100}{x - 30} = \frac{60}{x + 30}$

查看试题解析
13. 某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道，为尽量减少施工对交通造成的影响，实施施工时“…”，设实际每天铺设管道x米，则可得方程 $\frac{3000}{x - 10} - \frac{3000}{x} = 15$ ，根据此情景，题中用“…”表示的缺失的条件应补为（）

A、每天比原计划多铺设10米，结果延期15天才完成 B、每天比原计划少铺设10米，结果延期15天才完成 C、每天比原计划多铺设10米，结果提前15天才完成 D、每天比原计划少铺设10米，结果提前15天才完成

查看试题解析
14. 某开发区在一项工程招标时，接到甲、乙两个工程队的投标书，工程领导小组根据甲、乙两队的投标书测算，可有三种施工方案：①甲队单独完成这项工程，刚好如期完成；②乙队单独完成此项工程要比规定工期多用5天；③ ，剩下的工程由乙队单独做，也正好如期完工.小亮设规定的工期为x天，根据题意列出了方程： $\frac{4}{x} + \frac{x}{x + 5} = 1$ ，则方案③中被墨水污染的部分应该是（）

A、甲先做了4天 B、甲乙合作了4天 C、甲先做了工程的 $\frac{1}{4}$ D、甲乙合作了工程的 $\frac{1}{4}$

查看试题解析

二、填空题

15. 分式方程 $\frac{2}{x - 3}$ = $\frac{3}{x - 2}$ 的解是x= ．

查看试题解析
16. 若关于x的方程﹣2x+m $\sqrt{2017 - x}$ +4020=0存在整数解，则正整数m的所有取值的和为．

查看试题解析
17. 在正数范围内定义一种运算“※”，其规则为a※b= $\frac{1}{a}$ + $\frac{1}{b}$ ，如2※4= $\frac{1}{2}$ + $\frac{1}{4}$ = $\frac{3}{4}$ ．根据这个规则x※（﹣2x）= $\frac{3}{2}$ 的解为．

查看试题解析
18. 某水果店搞促销活动，对某种水果打8折出售，若用60元钱买这种水果，可以比打折前多买3斤．设该种水果打折前的单价为x元，根据题意可列方程为．

查看试题解析
19. 某市为绿化环境计划植树2400棵，实际劳动中每天植树的数量比原计划多20%，结果提前8天完成任务．若设原计划每天植树x棵，则根据题意可列方程为．

查看试题解析
20. 某市为治理污水，需要铺设一段全长为3000m的污水排放管道．为了尽量减少施工对城市交通所造成的影响，实际施工时每天的工效比原计划增加25%，结果提前15天完成这一任务．则实际每天铺设污水排放管道的长度为 m．

查看试题解析

三、计算题

21. 解下列方程

(1)、 $\frac{6 x}{x + 2} - 2 = 0$

(2)、 $\frac{3}{x - 2} = \frac{2}{x} + \frac{6}{x^{2} - 2 x}$

查看试题解析
22. 当x为何值时，分式 $\frac{3 - x}{2 - x}$ 的值比分式 $\frac{1}{x - 2}$ 的值大3？

查看试题解析

四、综合题

23. 如图，Rt△ABC中，∠B=90°，AB=3cm，BC=4cm．点D在AC上，AD=1cm，点P从点A出发，沿AB匀速运动；点Q从点C出发，沿C→B→A→C的路径匀速运动．两点同时出发，在B点处首次相遇后，点P的运动速度每秒提高了2cm，并沿B→C→A的路径匀速运动；点Q保持速度不变，并继续沿原路径匀速运动，两点在D点处再次相遇后停止运动，设点P原来的速度为xcm/s．

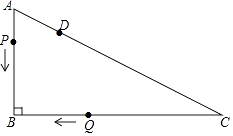(1)、点Q的速度为cm/s（用含x的代数式表示）．

(2)、求点P原来的速度．

查看试题解析
24. 某同学准备购买笔和本子送给农村希望小学的同学，在市场上了解到某种本子的单价比某种笔的单价少4元，且用30元买这种本子的数量与用50元买这种笔的数量相同．

(1)、求这种笔和本子的单价；

(2)、该同学打算用自己的100元压岁钱购买这种笔和本子，计划100元刚好用完，并且笔和本子都买，请列出所有购买方案．

查看试题解析

备考2018年中考数学一轮基础复习：专题九 分式方程

一、单选题

二、填空题

三、计算题

四、综合题

备考2018年中考数学一轮基础复习：专题九分式方程