河北省衡水金卷2018年普通高等学校理数招生全国统一考试模拟试题(2)
试卷更新日期:2018-03-19 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 已知 ,且 是虚数单位, ,则 ( )A、4 B、 C、 D、3. 已知 为直线 的倾斜角,若 ,则直线 的斜率为( )A、3 B、-4 C、 D、4. 双曲线 的渐近线与抛物线 相切,则双曲线的离心率为( )A、 B、 C、 D、5. 袋中装有4个红球、3个白球,甲、乙按先后次序无放回地各摸取一球,在甲摸到了白球的条件下,乙摸到白球的概率是( )A、 B、 C、 D、6. 《算法统宗》是中国古代数学名著,由程大位所著,其中记载这样一首诗:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?请君布算莫迟疑!其含义为:用九百九十九文钱共买了一千个甜果和苦果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个,请问究竟甜、苦果各有几个?现有如图所示的程序框图,输入 分别代表钱数和果子个数,则符合输出值 的为( )
 A、 为甜果数343 B、 为苦果数343 C、 为甜果数657 D、 为苦果数6577. 在区间 内的所有零点之和为( )A、 B、 C、 D、8. 已知 恒成立,若 为真命题,则实数 的最小值为( )A、2 B、3 C、4 D、59. 已知某几何体的三视图如图所示,则该几何体的体积为( )
A、 为甜果数343 B、 为苦果数343 C、 为甜果数657 D、 为苦果数6577. 在区间 内的所有零点之和为( )A、 B、 C、 D、8. 已知 恒成立,若 为真命题,则实数 的最小值为( )A、2 B、3 C、4 D、59. 已知某几何体的三视图如图所示,则该几何体的体积为( ) A、 B、 C、 D、10. 如图为正方体 ,动点 从 点出发,在正方体表面上沿逆时针方向运动一周后,再回到 ,运动过程种,点 与平面 的距离保持不变,运动的路程 与 之间满足函数关系 ,则此函数图象大致是( )
A、 B、 C、 D、10. 如图为正方体 ,动点 从 点出发,在正方体表面上沿逆时针方向运动一周后,再回到 ,运动过程种,点 与平面 的距离保持不变,运动的路程 与 之间满足函数关系 ,则此函数图象大致是( ) A、
A、 B、
B、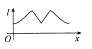 C、
C、 D、
D、 11. 抛物线 的准线交 轴于点 ,过点 的直线交抛物线于 两点, 为抛物线的焦点,若 ,则直线 的斜率 为( )A、2 B、 C、 D、12. 已知函数 ,其中 为自然对数的底数,若 有两个零点,则实数 的取值范围是( )A、 B、 C、 D、
11. 抛物线 的准线交 轴于点 ,过点 的直线交抛物线于 两点, 为抛物线的焦点,若 ,则直线 的斜率 为( )A、2 B、 C、 D、12. 已知函数 ,其中 为自然对数的底数,若 有两个零点,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 若向量 , 是椭圆 上的动点,则 的最小值为 .14. 已知 满足 ,则 的取值范围是 .15. 中,角 的对边分别为 ,当 最大时, .16. 3位逻辑学家分配10枚金币,因为都对自己的逻辑能力很自信,决定按以下方案分配:
(1)抽签确定各人序号:1,2,3;
(2)1号提出分配方案,然后其余各人进行表决,如果方案得到不少于半数的人同意(提出方案的人默认同意自己方案),就按照他的方案进行分配,否则1好只得到2枚金币,然后退出分配与表决;
(3)再由2号提出方案,剩余各人进行表决,当且仅当不少于半数的人同意时(提出方案的人默认同意自己方案),才会按照他的提案进行分配,否则也将得到2枚金币,然后退出分配与表决;
(4)最后剩的金币都给3号.每一位逻辑学家都能够进行严密的逻辑推理,并能很理智的判断自身的得失,1号为得到最多的金币,
提出的分配方案中1号、2号、3号所得金币的数量分别为 .
三、解答题
-
17. 已知数列 满足 ,且 .(1)、求数列 的通项公式;(2)、求 的值.18. 某校高三年级有1000人,某次考试不同成绩段的人数 ,且所有得分都是整数.
参考数据: .
(1)、求全班平均成绩;(2)、计算得分超过141的人数;(精确到整数)(3)、甲同学每次考试进入年级前100名的概率是 ,若本学期有4次考试, 表示进入前100名的次数,写出 的分布列,并求期望与方差.19. 已知在直角梯形 中, , ,将 沿 折起至 ,使二面角 为直角. (1)、求证:平面 平面 ;(2)、若点 满足 , ,当二面角 为45°时,求 的值.20. 如图,矩形 中, 且 , 交 于点 .
(1)、求证:平面 平面 ;(2)、若点 满足 , ,当二面角 为45°时,求 的值.20. 如图,矩形 中, 且 , 交 于点 . (1)、若点 的轨迹是曲线 的一部分,曲线 关于 轴、 轴、原点都对称,求曲线 的轨迹方程;(2)、过点 作曲线 的两条互相垂直的弦 ,四边形 的面积为 ,探究 是否为定值?若是,求出此定值,若不是,请说明理由.
(1)、若点 的轨迹是曲线 的一部分,曲线 关于 轴、 轴、原点都对称,求曲线 的轨迹方程;(2)、过点 作曲线 的两条互相垂直的弦 ,四边形 的面积为 ,探究 是否为定值?若是,求出此定值,若不是,请说明理由.