2017-2018学年高中文数高考复习专题03:函数的应用
试卷更新日期:2018-03-19 类型:二轮复习
一、单选题
-
1. 已知奇函数f(x)是R上的单调函数,若函数y=f(2x2+1)+f(λ-x)只有一个零点,则实数λ的值是( )A、 B、 C、 D、2. 已知函数f(x)=(m2-m-5)xm是幂函数,且在x∈(0,+∞)上为增函数,则实数m的值是( )A、-2 B、4 C、3 D、-2或33. 某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示,已知该年的平均气温为10 ℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 已知a,b,c,d都是常数,a>b,c>d.若f(x)=2 017-(x-a)(x-b)的零点为c,d,则下列不等式正确的是( )A、a>c>b>d B、a>b>c>d C、c>d>a>b D、c>a>b>d5. 已知函数 ,在下列区间中,包含f(x)零点的区间是( )
4. 已知a,b,c,d都是常数,a>b,c>d.若f(x)=2 017-(x-a)(x-b)的零点为c,d,则下列不等式正确的是( )A、a>c>b>d B、a>b>c>d C、c>d>a>b D、c>a>b>d5. 已知函数 ,在下列区间中,包含f(x)零点的区间是( )
A、(0,1) B、(1,2) C、(2,4) D、(4,+∞)6. 已知f(x)是偶函数,当x>0时,f(x)单调递减,设a=-21.2 , ,c=2log52,则f(a),f(b),f(c)的大小关系为( )A、f(c)<f(b)<f(a) B、f(c)<f(a)<f(b) C、f(c)>f(b)>f(a) D、f(c)>f(a)>f(b)7. 若函数y=f(x)的图象上存在不同的两点M、N关于原点对称,则称点对(M,N)是函数y=f(x)的一对“和谐点对”(点对(M,N)与(N,M)看作同一对“和谐点对”).已知函数 ,则此函数的“和谐点对”有( )A、1对 B、2对 C、3对 D、4对8. 已知 , , ,则实数a,b,c的大小关系是( )A、a>c>b B、b>a>c C、a>b>c D、c>b>a9. 函数y=ax+2-1(a>0且a≠1)的图象恒过的点是( )A、(0,0) B、(0,-1) C、(-2,0) D、(-2,-1)10. 函数y= 的图象大致是( )A、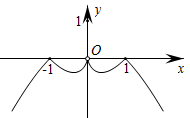
B、
B、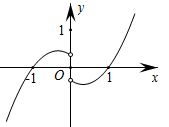
C、
C、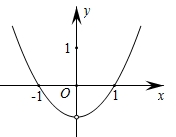
D、
D、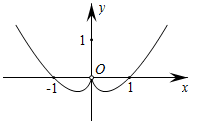
11. 设函数 ,若f(a)<1,则实数a的取值范围是( )A、(-∞,-3) B、(1,+∞) C、(-3,1) D、(-∞,-3)∪(1,+∞)12. 某动物数量y(只)与时间x(年)的关系为y=alog2(x+1),设第一年有100只,则到第七年它们发展到( )A、300只 B、400只 C、500只 D、600只
11. 设函数 ,若f(a)<1,则实数a的取值范围是( )A、(-∞,-3) B、(1,+∞) C、(-3,1) D、(-∞,-3)∪(1,+∞)12. 某动物数量y(只)与时间x(年)的关系为y=alog2(x+1),设第一年有100只,则到第七年它们发展到( )A、300只 B、400只 C、500只 D、600只二、填空题
-
13. 已知函数 ,关于 的方程 有且只有一个实根,则实数 的取值范围是 .14. 已知函数f(x)=|log3x|,实数m,n满足0<m<n,且f(m)=f(n),若f(x)在[m2 , n]上的最大值为2,则 .15. 某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量P(毫克/升)与时间t(小时)的关系为P=P0e-kt.如果在前5小时消除了10%的污染物,那么污染物减少19%需要花费的时间为小时.16. + = .
三、解答题
-
17. 在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.
 (1)、当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;(2)、企业乙只依靠该店,最早可望在几年后脱贫?
(1)、当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;(2)、企业乙只依靠该店,最早可望在几年后脱贫?