2017-2018学年中考数学专题题型复习11：最值问题
试卷更新日期：2018-03-19 类型：二轮复习
一、单选题
-
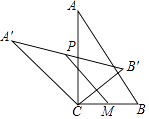
1. 如图，在Rt△ABC中，∠ACB=90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC=2，∠BAC=30°，则线段PM的最大值是（ ）
A、4 B、3 C、2 D、12.如图，点A（a，3），B（b，1）都在双曲线y= 上，点C，D，分别是x轴，y轴上的动点，则四边形ABCD周长的最小值为（ ）
A、 B、 C、 D、3. 如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（ ）
A、 B、2 C、2 D、二、填空题
-
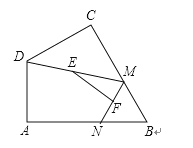
4.
如图，四边形ABCD中，∠A=90°，AB=3 ， AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为 ．
5.如图所示，正方形ABCD的边长为6，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为 ．
6.如图，正方形ABCD的边长为1，中心为点O，有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转，在旋转过程中，这个正六边形始终在正方形ABCD内（包括正方形的边），当这个正六边形的边长最大时，AE的最小值为 ．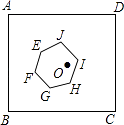
7.如图，AB是⊙O的弦，AB=6，点C是⊙O上的一个动点，且∠ACB=45°．若点M，N分别是AB，BC的中点，则MN长的最大值是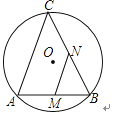
三、综合题
-
8.
如图，将边长为6的正三角形纸片ABC按如下顺序进行两次折叠，展平后，得折痕AD，BE（如图①），点O为其交点．
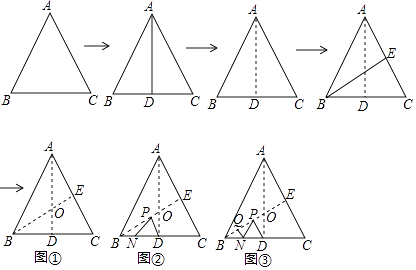(1)、探求AO到OD的数量关系，并说明理由；(2)、如图②，若P，N分别为BE，BC上的动点．（Ⅰ）当PN+PD的长度取得最小值时，求BP的长度；
（Ⅱ）如图③，若点Q在线段BO上，BQ=1，则QN+NP+PD的最小值= ．