2017-2018学年中考数学专题题型复习09:规律与猜想
试卷更新日期:2018-03-19 类型:二轮复习
一、单选题
-
1.
如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为a1 , 第2幅图形中“●”的个数为a2 , 第3幅图形中“●”的个数为a3 , …,以此类推,则 + + +…+ 的值为( )
 A、 B、 C、 D、2.
A、 B、 C、 D、2.如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
 A、2017π B、2034π C、3024π D、3026π3.
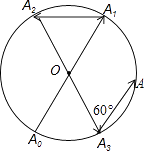
A、2017π B、2034π C、3024π D、3026π3.如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;…按此规律运动到点A2017处,则点A2017与点A0间的距离是( )
 A、4 B、2 C、2 D、04.
A、4 B、2 C、2 D、04.下列图象都是由相同大小的
 按一定规律组成的,其中第①个图形中一共有4颗
按一定规律组成的,其中第①个图形中一共有4颗 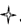 ,第②个图形中一共有11颗
,第②个图形中一共有11颗 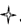 ,第③个图形中一共有21颗
,第③个图形中一共有21颗 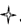 ,…,按此规律排列下去,第⑨个图形中
,…,按此规律排列下去,第⑨个图形中 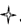 的颗数为( )
的颗数为( )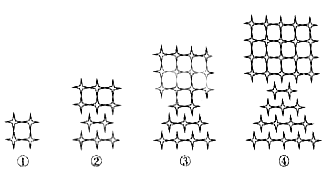 A、116 B、144 C、145 D、1505. 观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( )
A、116 B、144 C、145 D、1505. 观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,…将这种做法继续下去(如图2,图3…),则图6中挖去三角形的个数为( )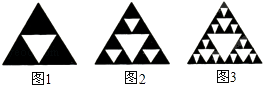 A、121 B、362 C、364 D、7296.
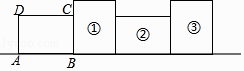
A、121 B、362 C、364 D、7296.一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形.在满足条件的所有分割中,若知道九个小矩形中n个小矩形的周长,就一定能算出这个在大矩形的面积,则n的最小值是 ( )
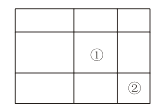 A、3 B、4 C、5 D、67. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
A、3 B、4 C、5 D、67. 我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.
根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )
A、2017 B、2016 C、191 D、1908. 中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初日健步不为难,次日脚痛减一半,六朝才得到其关.”其大意是,有人要去某关口,路程为378里,第一天健步行走,从第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,则此人第六天走的路程为( )A、24里 B、12里 C、6里 D、3里9.在每个小正方形的边长为 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 的另一个格点的运动称为一次跳马变换.例如,在 的正方形网格图形中(如图1),从点 经过一次跳马变换可以到达点 , , , 等处.现有 的正方形网格图形(如图2),则从该正方形的顶点 经过跳马变换到达与其相对的顶点 ,最少需要跳马变换的次数是( )
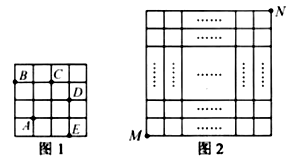 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
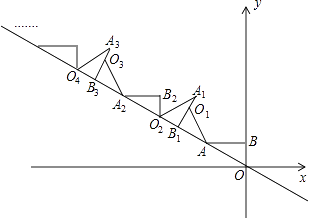
10. 如图,AB⊥y轴,垂足为B,将△ABO绕点A逆时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=﹣ x上,再将△AB1O1绕点B1逆时针旋转到△A1B1O1的位置,使点O1的对应点O2落在直线y=﹣ x上,依次进行下去…若点B的坐标是(0,1),则点O12的纵坐标为 .
 11.
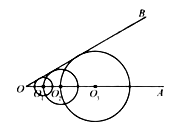
11.如图,已知 ,在射线 上取点 ,以 为圆心的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切; ;在射线 上取点 ,以 为圆心, 为半径的圆与 相切.若 的半径为 ,则 的半径长是 .
 12.
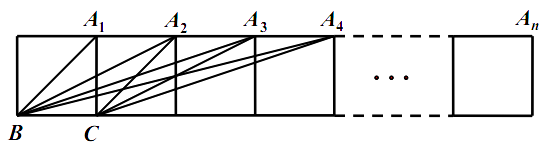
12.如图,把 个边长为1的正方形拼接成一排,求得 , , ,计算 , ……按此规律,写出 (用含 的代数式表示).
 13.
13.如图,正△ABO的边长为2,O为坐标原点,A在 轴上,B在第二象限。△ABO沿 轴正方向作无滑动的翻滚,经第一次翻滚后得△A1B1O,则翻滚3次后点B的对应点的坐标是;翻滚2017次后AB中点M经过的路径长为.
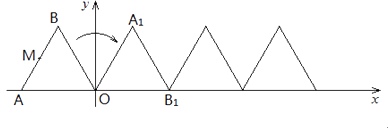 14.
14.把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2C垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为 .
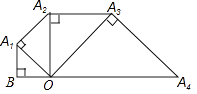
 15. 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .
15. 如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .