2017-2018学年中考数学专题题型复习08:图形变换有关的计算与证明
试卷更新日期:2018-03-19 类型:二轮复习
一、单选题
-
1. 如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
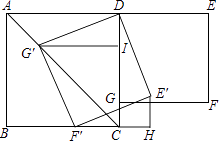 A、 B、 C、 D、2. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )
A、 B、 C、 D、2. 在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),顶点A的坐标为(0,2),顶点B恰好落在第一象限的双曲线上,现将直角三角板沿x轴正方向平移,当顶点A恰好落在该双曲线上时停止运动,则此时点C的对应点C′的坐标为( )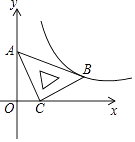 A、( ,0) B、(2,0) C、( ,0) D、(3,0)
A、( ,0) B、(2,0) C、( ,0) D、(3,0)二、填空题
-
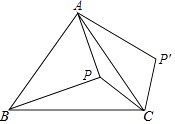
3. 如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为 .
 4.
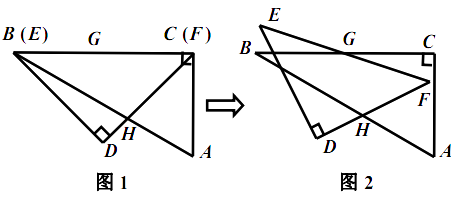
4.一副含 和 角的三角板 和 叠合在一起,边 与 重合, (如图1),点 为边 的中点,边 与 相交于点 ,此时线段 的长是 . 现将三角板 绕点 按顺时针方向旋转(如图2),在 从 到 的变化过程中,点 相应移动的路径长共为 . (结果保留根号)
 5. 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 .
5. 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 .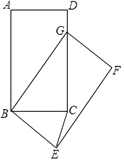 6. 如图,在正方形ABCD中,AD=2 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 .
6. 如图,在正方形ABCD中,AD=2 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 . 7. 两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=cm.
7. 两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=cm.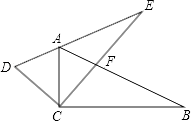 8. 如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .
8. 如图,正方形OABC的边长为2,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是 .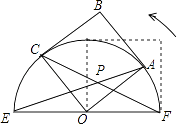 9. 已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于 .10. 如图,在矩形ABCD中,AB= , AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为 .
9. 已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于 .10. 如图,在矩形ABCD中,AB= , AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为 .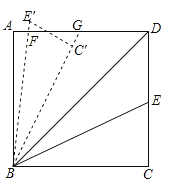 11. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是
11. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= ,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是
三、综合题
-
12. 如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0, ).
 (1)、求∠BAO的度数;(2)、如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
(1)、求∠BAO的度数;(2)、如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?(3)、若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.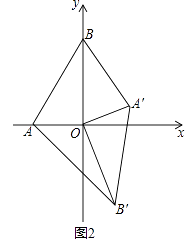 13. 如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.(1)、如图1,若CE=CF,求证:DE=DF;
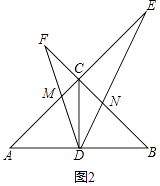
13. 如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.(1)、如图1,若CE=CF,求证:DE=DF;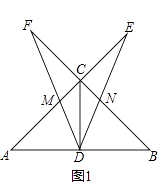 (2)、如图2,在∠EDF绕点D旋转的过程中:
(2)、如图2,在∠EDF绕点D旋转的过程中:①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
 14. 如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
14. 如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.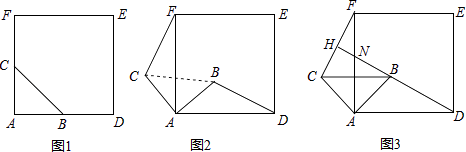 (1)、当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;(2)、当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
(1)、当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;(2)、当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.①求证:BD⊥CF;
②当AB=2,AD=3 时,求线段DH的长.
15. 如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.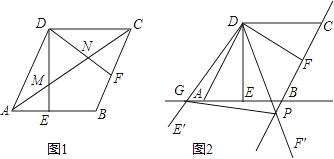 (1)、如图1,连接AC分别交DE、DF于点M、N,求证:MN= AC;(2)、如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3 时,求旋转角的大小并指明旋转方向.
(1)、如图1,连接AC分别交DE、DF于点M、N,求证:MN= AC;(2)、如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3 时,求旋转角的大小并指明旋转方向.四、解答题
-
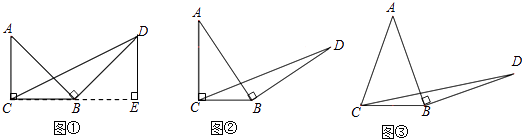
16. 问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE,
易证△ABC≌△BDE,从而得到△BCD的面积为 .
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)
 17. 已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
17. 已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系,QE与QF的数量关系.
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
