2017-2018学年中考数学专题题型复习07:圆的有关计算与证明
试卷更新日期:2018-03-19 类型:二轮复习
一、解答题
-
1.
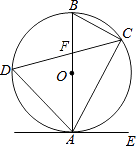
如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9
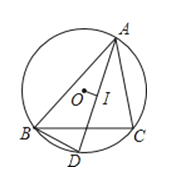
 (1)、求证:△COD∽△CBE;(2)、求半圆O的半径 的长2. 如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.
(1)、求证:△COD∽△CBE;(2)、求半圆O的半径 的长2. 如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.(1)求证:BD=DI;
(2)若OI⊥AD,求的值.
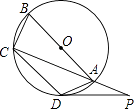
 3. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
3. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.(Ⅰ)若AB=4,求 的长;
(Ⅱ)若 = ,AD=AP,求证:PD是⊙O的切线.
 4. 如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.
4. 如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC.(Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DF•DA.
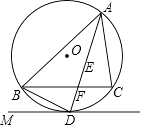 5.
5.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
 (1)、求证:AC平分∠DAO.(2)、若∠DAO=105°,∠E=30°.
(1)、求证:AC平分∠DAO.(2)、若∠DAO=105°,∠E=30°.①求∠OCE的度数.
②若⊙O的半径为2 ,求线段EF的长.
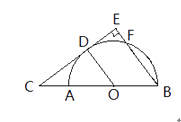
6.如图, 为 的直角边 上一点,以 为半径的 与斜边 相切于点 ,交 于点 .已知 , .
 (1)、求 的长;(2)、求图中阴影部分的面积.7. 如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)、求 的长;(2)、求图中阴影部分的面积.7. 如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径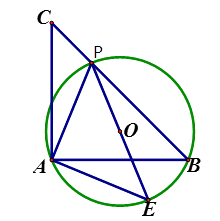 (1)、求证:△APE是等腰直角三角形;(2)、若⊙O的直径为2,求 的值
(1)、求证:△APE是等腰直角三角形;(2)、若⊙O的直径为2,求 的值二、综合题
-
8. 如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
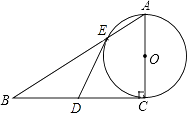 (1)、求证:DE是⊙O的切线;(2)、若AE:EB=1:2,BC=6,求AE的长.9. 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)、求证:DE是⊙O的切线;(2)、若AE:EB=1:2,BC=6,求AE的长.9. 如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.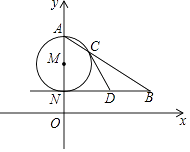 (1)、若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;(2)、若D为线段NB的中点,求证:直线CD是⊙M的切线.10. 如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
(1)、若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;(2)、若D为线段NB的中点,求证:直线CD是⊙M的切线.10. 如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.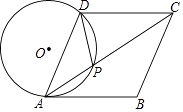 (1)、求证:AB是⊙O的切线;(2)、若AC=8,tan∠BAC= ,求⊙O的半径.11. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)、求证:AB是⊙O的切线;(2)、若AC=8,tan∠BAC= ,求⊙O的半径.11. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE. (1)、求证:BE与⊙O相切;(2)、设OE交⊙O于点F,若DF=1,BC=2 ,求阴影部分的面积.12. 如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.
(1)、求证:BE与⊙O相切;(2)、设OE交⊙O于点F,若DF=1,BC=2 ,求阴影部分的面积.12. 如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD. (1)、求证:△ACD∽△BAD;(2)、求证:AD是⊙O的切线.13. 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
(1)、求证:△ACD∽△BAD;(2)、求证:AD是⊙O的切线.13. 如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G. (1)、求证:BC是⊙F的切线;(2)、若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;(3)、试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.14. 如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.
(1)、求证:BC是⊙F的切线;(2)、若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;(3)、试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.14. 如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.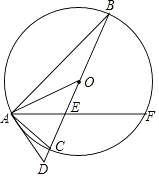 (1)、求证:AD是⊙O的切线;(2)、若⊙O的半径为5,CE=2,求EF的长.15. 如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.
(1)、求证:AD是⊙O的切线;(2)、若⊙O的半径为5,CE=2,求EF的长.15. 如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点. (1)、求证:PT2=PA•PB;(2)、若PT=TB= ,求图中阴影部分的面积.16. 如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)、求证:PT2=PA•PB;(2)、若PT=TB= ,求图中阴影部分的面积.16. 如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.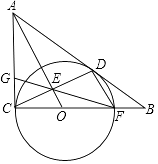 (1)、求证:DF∥AO;(2)、若AC=6,AB=10,求CG的长.17. 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)、求证:DF∥AO;(2)、若AC=6,AB=10,求CG的长.17. 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.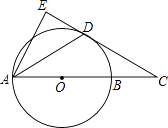 (1)、求证:直线CE是⊙O的切线.(2)、若BC=3,CD=3 ,求弦AD的长.18. 如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)、求证:直线CE是⊙O的切线.(2)、若BC=3,CD=3 ,求弦AD的长.18. 如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.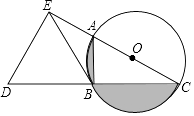 (1)、求证:BE是⊙O的切线;(2)、当BE=3时,求图中阴影部分的面积.19. 如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)、求证:BE是⊙O的切线;(2)、当BE=3时,求图中阴影部分的面积.19. 如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. (1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.20. 已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)、如图①,求∠T和∠CDB的大小;
(1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.20. 已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)、如图①,求∠T和∠CDB的大小;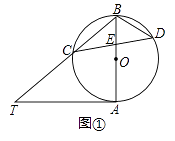 (2)、如图②,当BE=BC时,求∠CDO的大小.
(2)、如图②,当BE=BC时,求∠CDO的大小.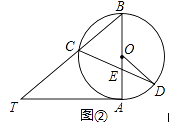 21. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD.
21. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF∥AB,与过点B的切线交于点F,连接BD. (1)、求证:BD=BF;(2)、若AB=10,CD=4,求BC的长.22. 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E, =
(1)、求证:BD=BF;(2)、若AB=10,CD=4,求BC的长.22. 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E, =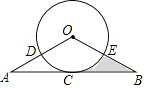 (1)、求证:OA=OB;(2)、已知AB=4 ,OA=4,求阴影部分的面积.23. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,
(1)、求证:OA=OB;(2)、已知AB=4 ,OA=4,求阴影部分的面积.23. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,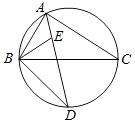 (1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.24. 如图,点E在以AB为直径的⊙O上,点C是 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.
(1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.24. 如图,点E在以AB为直径的⊙O上,点C是 的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.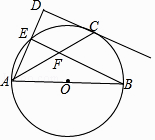 (1)、求证:CD是⊙O的切线;(2)、若cos∠CAD= ,BF=15,求AC的长.25. 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)、求证:CD是⊙O的切线;(2)、若cos∠CAD= ,BF=15,求AC的长.25. 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.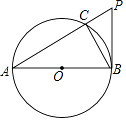 (1)、求证:∠BAC=∠CBP;(2)、求证:PB2=PC•PA;(3)、当AC=6,CP=3时,求sin∠PAB的值.
(1)、求证:∠BAC=∠CBP;(2)、求证:PB2=PC•PA;(3)、当AC=6,CP=3时,求sin∠PAB的值.