2017-2018学年中考数学专题题型复习06：四边形有关的计算与证明
试卷更新日期：2018-03-19 类型：二轮复习
一、解答题
-
1.
在一次课题学习中，老师让同学们合作编题．某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解．
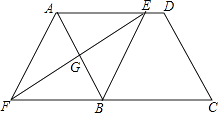
如图，将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H，使得AE＝CG，BF＝DH，连结EF、FG、GH、HE．
(1)、求证：四边形EFGH为平行四边形；(2)、若矩形ABCD是边长为1的正方形，且∠FEB＝45°，tan∠AEH＝2，求AE的长．2. 已知，如图，平行四边形ABCD中，E是BC边的中点，连DE并延长交AB的延长线于点F，求证：AB=BF．
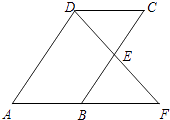3. 如图，点E，F分别在菱形ABCD的边DC，DA上，且CE=AF．求证：∠ABF=∠CBE．
4. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证．（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》）
请根据该图完成这个推论的证明过程．
证明：S矩形NFGD=S△ADC﹣（S△ANF+S△FGC），S矩形EBMF=S△ABC﹣（+）．
易知，S△ADC=S△ABC ， = ， = ．
可得S矩形NFGD=S矩形EBMF ．
5. 如图，在▱ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于 BF的相同长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF，则所得四边形ABEF是菱形．（Ⅰ）根据以上尺规作图的过程，求证：四边形ABEF是菱形；
（Ⅱ）若菱形ABEF的周长为16，AE=4 ，求∠C的大小．
6.如图，菱形ABCD中，DE⊥AB于E，DF⊥BC于F．
（1）求证：△ADE≌△CDF；
（2）若∠EDF=50°，求∠BEF的度数．
7. 如图，E是▱ABCD的边AD的中点，连接CE并延长交BA的延长线于F，若CD=6，求BF的长．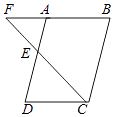
8. 如图，四边形ABCD是正方形，E、F分别是了AB、AD上的一点，且BF⊥CE，垂足为G，求证：AF=BE．
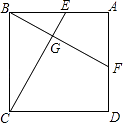9.定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
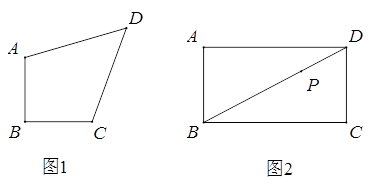(1)、如图1，等腰直角四边形ABCD，AB=BC，∠ABC=90°，①若AB=CD=1，AB//CD，求对角线BD的长.
②若AC⊥BD，求证：AD=CD.
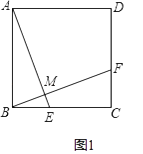
(2)、如图2，在矩形ABCD中，AB=5，BC=9，点P是对角线BD上一点，且BP=2PD，过点P作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形.求AE的长.10. 如图示，正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上，EF与BC相交于点G，连接CF．①求证：△DAE≌△DCF；
②求证：△ABG∽△CFG．
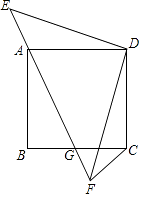11. 如图，在▱ABCD中，BE⊥AC，垂足E在CA的延长线上，DF⊥AC，垂足F在AC的延长线上，求证：AE=CF．
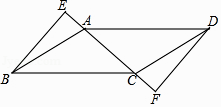12. 如图，四边形ABCD是平行四边形，E，F是对角线BD上的两点，且BF=ED，求证：AE∥CF．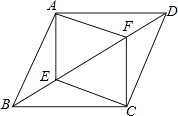
二、综合题
-
13. 如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．
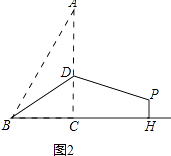
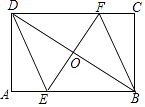(1)、求证：四边形BEDF是平行四边形；(2)、当四边形BEDF是菱形时，求EF的长．14. 已知，在Rt△ABC中，∠ACB=90°，AC=4，BC=2，D是AC边上的一个动点，将△ABD沿BD所在直线折叠，使点A落在点P处．(1)、如图1，若点D是AC中点，连接PC．
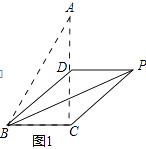
①写出BP，BD的长；
②求证：四边形BCPD是平行四边形．
(2)、如图2，若BD=AD，过点P作PH⊥BC交BC的延长线于点H，求PH的长．
15. 如图，DB∥AC，且DB= AC，E是AC的中点，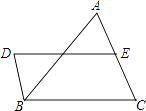
(1)、求证：BC=DE；(2)、连接AD、BE，若要使四边形DBEA是矩形，则给△ABC添加什么条件，为什么？16. 如图，四边形ABCD是正方形，△EBC是等边三角形．
(1)、求证：△ABE≌△DCE；(2)、求∠AED的度数．17. 如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．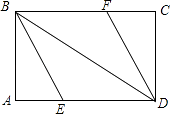
(1)、求证：四边形BEDF是平行四边形；(2)、当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．18.如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．
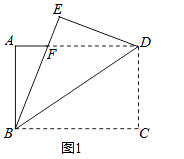(1)、求证：△BDF是等腰三角形；(2)、如图2，过点D作DG∥BE，交BC于点G，连接FG交BD于点O．
①判断四边形BFDG的形状，并说明理由；
②若AB=6，AD=8，求FG的长．
19. 如图，在▱ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC．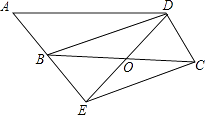
(1)、求证：四边形BECD是平行四边形；(2)、若∠A=50°，则当∠BOD=°时，四边形BECD是矩形．20. 如图，在四边形ABCD中，BD为一条对角线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，连接BE．
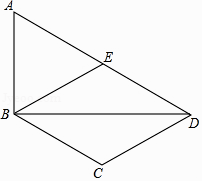(1)、求证：四边形BCDE为菱形；(2)、连接AC，若AC平分∠BAD，BC=1，求AC的长．21. 将一个直角三角形纸片ABO放置在平面直角坐标系中，点 ，点B（0，1），点O（0，0）．P是边AB上的一点（点P不与点A，B重合），沿着OP折叠该纸片，得点A的对应点A'．(1)、如图①，当点A'在第一象限，且满足A'B⊥OB时，求点A'的坐标；
(2)、如图②，当P为AB中点时，求A'B的长；
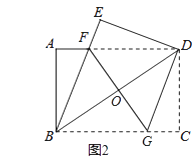
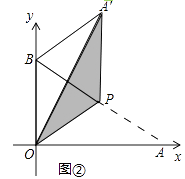(3)、当∠BPA'=30°时，求点P的坐标（直接写出结果即可）．22. 已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF．
(1)、求证：△BCE≌△DCF；(2)、当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．23. 如图，已知BA=AE=DC，AD=EC，CE⊥AE，垂足为E．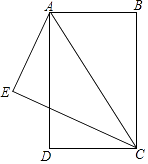
(1)、求证：△DCA≌△EAC；(2)、只需添加一个条件，即 ， 可使四边形ABCD为矩形．请加以证明．24.如图，在正方形ABCD中，点E、G分别是边AD、BC的中点，AF= AB．
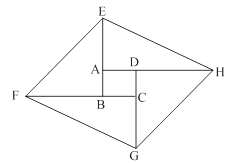
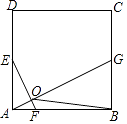(1)、求证：EF⊥AG；(2)、若点F、G分别在射线AB、BC上同时向右、向上运动，点G运动速度是点F运动速度的2倍，EF⊥AG是否成立（只写结果，不需说明理由）？(3)、正方形ABCD的边长为4，P是正方形ABCD内一点，当S△PAB=S△OAB ， 求△PAB周长的最小值．25. 如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交BC于G．
(1)、求证：BG=DE；(2)、若点G为CD的中点，求 的值．26.如图，在△ABC中，点O是边AC上一个动点，过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．
(1)、若CE=8，CF=6，求OC的长；(2)、连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．
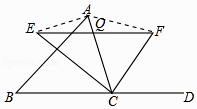27. 如图所示，已知四边形ABCD，ADEF都是菱形，∠BAD=∠FAD，∠BAD为锐角．
(1)、求证：AD⊥BF；(2)、若BF=BC，求∠ADC的度数．28. 如图，矩形ABCD的对角线AC，BD相交于点O，点E，F在BD上，BE=DF．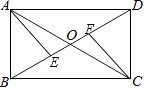
(1)、求证：AE=CF；(2)、若AB=6，∠COD=60°，求矩形ABCD的面积．29. 如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD．
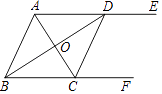(1)、求证：四边形ABCD是菱形；(2)、若∠ADB=30°，BD=6，求AD的长．30.边长为2 的正方形ABCD中，P是对角线AC上的一个动点（点P与A、C不重合），连接BP，将BP绕点B顺时针旋转90°到BQ，连接QP，QP与BC交于点E，QP延长线与AD（或AD延长线）交于点F．
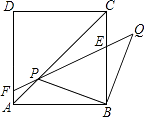(1)、连接CQ，证明：CQ=AP；(2)、设AP=x，CE=y，试写出y关于x的函数关系式，并求当x为何值时，CE= BC；(3)、猜想PF与EQ的数量关系，并证明你的结论．31.如图，点B、E、C、F在一条直线上，AB=DF，AC=DE，BE=FC．
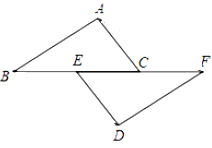(1)、求证：△ABC≌△DFE；
(2)、连接AF、BD，求证：四边形ABDF是平行四边形．32.矩形ABCD中，E、F分别是AD、BC的中点，CE、AF分别交BD于G、H两点．
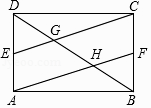
求证：
(1)、四边形AFCE是平行四边形；(2)、证明：EG=FH．33. 如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．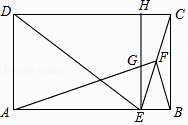
(1)、求证：DE=DC；(2)、求证：AF⊥BF；(3)、当AF•GF=28时，请直接写出CE的长．34.如图，已知矩形ABCD（AB＜AD）．
(1)、请用直尺和圆规按下列步骤作图，保留作图痕迹；①以点A为圆心，以AD的长为半径画弧交边BC于点E，连接AE；
②作∠DAE的平分线交CD于点F；
③连接EF；
(2)、在（1）作出的图形中，若AB=8，AD=10，则tan∠FEC的值为 ．35.如图，等腰三角形ABC中，BD，CE分别是两腰上的中线．
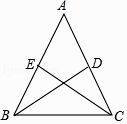(1)、求证：BD=CE；(2)、设BD与CE相交于点O，点M，N分别为线段BO和CO的中点，当△ABC的重心到顶点A的距离与底边长相等时，判断四边形DEMN的形状，无需说明理由．
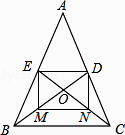36. 如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD∥BC，AC=8，BD=6，．
(1)、求证：四边形ABCD是平行四边形；(2)、若AC⊥BD，求▱ABCD的面积．37.已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．
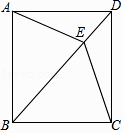(1)、求证：四边形ABCD是菱形；(2)、如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．
