2017-2018学年中考数学专题题型复习02：一次函数与反比例函数的综合

试卷更新日期：2018-03-16 类型：二轮复习

进入出卷网下载

一、解答题

1.
如图，一次函数y=x+1的图象与反比例函数y= $\frac{k}{x}$ （k为常数，且k≠0）的图象都经过点A（m，2）．
（1）求点A的坐标及反比例函数的表达式；
（2）设一次函数y=x+1的图象与x轴交于点B，若点P是x轴上一点，且满足△ABP的面积是2，直接写出点P的坐标．

查看试题解析
2.
如图，在平面直角坐标系中，一次函数y=ax+b的图象与反比例函数y= $\frac{k}{x}$ 的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，﹣2），tan∠BOC= $\frac{1}{2}$ ．
（1）求该反比例函数和一次函数的解析式．
（2）求△BOC的面积．
（3）P是x轴上的点，且△PAC的面积与△BOC的面积相等，求P点的坐标．

查看试题解析
3.
如图，直线y=x+1与y轴交于A点，与反比例函数y= $\frac{k}{x}$ （x＞0）的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO= $\frac{1}{2}$ ．
（1）求k的值；
（2）设点N（1，a）是反比例函数y= $\frac{k}{x}$ （x＞0）图象上的点，在y轴上是否存在点P，使得PM+PN最小？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析

二、综合题

4. 如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y= $\frac{m}{x}$ （m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，6），点C的坐标为（﹣2，0），且tan∠ACO=2．

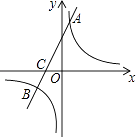(1)、求该反比例函数和一次函数的解析式；

(2)、求点B的坐标．

查看试题解析
5.
如图，一次函数y=kx+b（k＜0）与反比例函数y= $\frac{m}{x}$ 的图象相交于A、B两点，一次函数的图象与y轴相交于点C，已知点A（4，1）

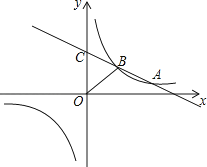(1)、求反比例函数的解析式；

(2)、连接OB（O是坐标原点），若△BOC的面积为3，求该一次函数的解析式．

查看试题解析
6.
如图，直线y= $\frac{1}{2}$ x+2与双曲线相交于点A（m，3），与x轴交于点C．

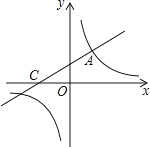(1)、求双曲线解析式；

(2)、点P在x轴上，如果△ACP的面积为3，求点P的坐标．

查看试题解析
7.
如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直与x轴，垂足为点B，反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过AO的中点C，且与AB相交于点D，OB=4，AD=3，

(1)、求反比例函数y= $\frac{k}{x}$ 的解析式；

(2)、求cos∠OAB的值；

(3)、求经过C、D两点的一次函数解析式．

查看试题解析
8.
在平面直角坐标系中，一次函数y=ax+b（a≠0）的图形与反比例函数y= $\frac{k}{x}$ （k≠0）的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH=3，tan∠AOH= $\frac{4}{3}$ ，点B的坐标为（m，﹣2）．

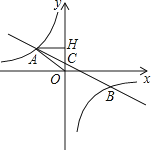(1)、求△AHO的周长；

(2)、求该反比例函数和一次函数的解析式．

查看试题解析
9.
如图，在平面直角坐标系xOy中，双曲线y= $\frac{π}{x}$ 与直线y=﹣2x+2交于点A（﹣1，a）．

(1)、求a，m的值；

(2)、求该双曲线与直线y=﹣2x+2另一个交点B的坐标．

查看试题解析
10.
如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数y= $\frac{m}{x}$ 的图象在第二象限交于点C，CE⊥x轴，垂足为点E，tan∠ABO= $\frac{1}{2}$ ，OB=4，OE=2．

(1)、求反比例函数的解析式；

(2)、若点D是反比例函数图象在第四象限上的点，过点D作DF⊥y轴，垂足为点F，连接OD、BF．如果S_△_BAF=4S_△_DFO ，求点D的坐标．

查看试题解析
11.
如图，一次函数y=kx+b的图象与反比例函数y= $\frac{m}{x}$ （x＞0）的图象交于A（2，﹣1），B（ $\frac{1}{2}$ ，n）两点，直线y=2与y轴交于点C．

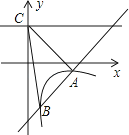(1)、求一次函数与反比例函数的解析式；

(2)、求△ABC的面积．

查看试题解析
12.
如图，在平面直角坐标系中A点的坐标为（8，y），AB⊥x轴于点B，sin∠OAB= $\frac{4}{5}$ ，反比例函数y= $\frac{k}{x}$ 的图象的一支经过AO的中点C，且与AB交于点D．

(1)、求反比例函数解析式

(2)、若函数y=3x与y= $\frac{k}{x}$ 的图象的另一支交于点M，求三角形OMB与四边形OCDB的面积的比

查看试题解析
13.
如图，一次函数y=kx+b（k＜0）的图象经过点C（3，0），且与两坐标轴围成的三角形的面积为3．

(1)、求该一次函数的解析式；

(2)、若反比例函数y= $\frac{m}{x}$ 的图象与该一次函数的图象交于二、四象限内的A、B两点，且AC=2BC，求m的值．

查看试题解析
14.
如图，正比例函数y=2x的图象与反比例函数y= $\frac{k}{x}$ 的图象交于A、B两点，过点A作AC垂直x轴于点C，连结BC．若△ABC的面积为2．

(1)、求k的值；

(2)、x轴上是否存在一点D ，使△ABD为直角三角形？若存在，求出点D的坐标；若不存在，请说明理由．

查看试题解析
15.
如图，反比例函数 $y = \frac{k}{x}$ （k＞0）与正比例函数y=ax相交于A（1，k），B（﹣k，﹣1）两点．

(1)、求反比例函数和正比例函数的解析式；

(2)、将正比例函数y=ax的图象平移，得到一次函数y=ax+b的图象，与函数 $y = \frac{k}{x}$ （k＞0）的图象交于C（x₁ ， y₁），D（x₂ ， y₂），且|x₁﹣x₂|•|y₁﹣y₂|=5，求b的值．

查看试题解析