备考2018年中考数学一轮基础复习:专题八 一元二次方程
试卷更新日期:2018-03-16 类型:一轮复习
一、单选题
-
1. 用公式法解方程4y2=12y+3,得到( )A、y= B、y= C、y= D、y=2. 一元二次方程x2﹣16=0的根是( )A、x=2 B、x=4 C、x1=2,x2=﹣2 D、x1=4,x2=﹣43. 用配方法解下列方程时,配方有错误的是( )
A、x2﹣2x﹣99=0化为(x﹣1)2=100 B、x2+8x+9=0化为(x+4)2=25 C、2t2﹣7t﹣4=0化为(t﹣)2= D、3x2﹣4x﹣2=0化为(x﹣)2=4. 一元二次方程式x2﹣8x=48可表示成(x﹣a)2=48+b的形式,其中a、b为整数,求a+b之值为何( )A、20 B、12 C、﹣12 D、﹣205. “一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,在论坛召开之际,福田欧辉陆续向缅甸仰光公交公司交付1000台清洁能源公交车,以2017客车海外出口第一大单的成绩,创下了客车行业出口之最,同时,这也是在国家“一带一路”倡议下,福田欧辉代表“中国制造”走出去的成果.预计到2019年,福田公司将向海外出口清洁能源公交车达到3000台.设平均每年的出口增长率为x,可列方程为( )A、1000(1+x%)2=3000 B、1000(1﹣x%)2=3000 C、1000(1+x)2=3000 D、1000(1﹣x)2=30006. 我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是( )A、x1=1,x2=3 B、x1=1,x2=﹣3 C、x1=﹣1,x2=3 D、x1=﹣1,x2=﹣37. 若关于x的一元二次方程(k+1)x2+2(k+1)x+k﹣2=0有实数根,则k的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、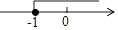 D、
D、 8. 若α、β为方程2x2﹣5x﹣1=0的两个实数根,则2α2+3αβ+5β的值为( )A、﹣13 B、12 C、14 D、159. 已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )A、有1对或2对 B、只有1对 C、只有2对 D、有2对或3对10. 三角形的两边a、b的夹角为60°且满足方程x2﹣3 x+4=0,则第三边的长是( )
8. 若α、β为方程2x2﹣5x﹣1=0的两个实数根,则2α2+3αβ+5β的值为( )A、﹣13 B、12 C、14 D、159. 已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )A、有1对或2对 B、只有1对 C、只有2对 D、有2对或3对10. 三角形的两边a、b的夹角为60°且满足方程x2﹣3 x+4=0,则第三边的长是( )
A、 B、2 C、2 D、311. 根据表格估计一元二次方程x2+2x﹣4=0的一个解的范围在( )x
﹣1
0
1
2
3
x2+2x﹣4
﹣5
﹣4
﹣1
4
11
A、﹣1<x<0 B、0<x<1 C、1<x<2 D、2<x<312. 如果一个等腰三角形的两边长分别为方程x2﹣5x+4=0的两根,则这个等腰三角形的周长为( )A、6 B、9 C、6或9 D、以上都不正确13. 若二次函数 的图像经过点 ,则关于 的方程 的实数根为( )A、 , B、 , C、 , D、 ,14. 关于x的一元二次方程(m﹣2)x2+2x+1=0有实数根,则m的取值范围是( )
A、m≤3 B、m<3 C、m<3且m≠2 D、m≤3且m≠215. 下面是某同学九年级期中测验中解答的几道填空题:(1)若x2=a,则x= a ;(2)方程x(x-1)=x-1的根是 x=0 ;(3)若直角三角形的两边长为x2-3x+2=0的两个根,则该三角形的面积为 1 ;(4)若关于x的一元二次方程3x2+k=0有实数根,则 k≤0 .其中答案完全正确的个数是( )
A、0个 B、1个 C、3个 D、4个二、填空题
-
16. 已知实数m满足m2﹣3m+1=0,则代数式m2+ 的值等于 .17. 已知关于x的一元二次方程x2﹣2(1﹣m)x+m2=0的两实数根为x1 , x2 , 则y=x1+x2+2x1x2的最小值为 .
18. 在实数范围内定义一种运算“﹡”,其规则为a﹡b=a2﹣b2 , 根据这个规则,求方程(x﹣2)﹡1=0的解为 .19. 小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2﹣2b+3,若将实数对(x,﹣3x)放入其中,得到一个新数为5,则x= .20. 为解决群众看病难的问题,一种药品连续两次降价,每盒的价格由原来的60元降至48.6元,则平均每次降价的百分率为 %.
三、计算题
-
21. (x+3)(x﹣1)=12(用配方法)22. 已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1 , x2 .(1)、求k的取值范围;(2)、若|x1+x2|=x1x2﹣1,求k的值.
四、综合题
-
23. 某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)、设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)
(2)、每件童装降价多少元时,平均每天赢利1200元.
(3)、要想平均每天赢利2000元,可能吗?请说明理由.
24. 已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动. (1)、如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?(2)、如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?(3)、在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
(1)、如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?(2)、如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?(3)、在(1)中,当P,Q出发几秒时,△PBQ有最大面积?