安徽省黄山2017-2018学年高三理数一模检测试卷
试卷更新日期:2018-03-16 类型:高考模拟
一、单选题
-
1. 集合 ,集合 ,则 等于( )A、 B、 C、 D、2. 已知复数 , , , 是虚数单位,若 是实数,则 ( )A、 B、 C、 D、3. 若双曲线 与直线 无交点,则离心率
 的取值范围是( ) A、 B、 C、 D、4. 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )
的取值范围是( ) A、 B、 C、 D、4. 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径的长度为( )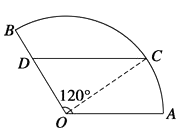 A、 B、 C、 D、5. 《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺 .问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”. 就是说:圆堡瑽(圆柱体)的体积为 (底面圆的周长的平方 高),则由此可推得圆周率 的取值为( )A、 B、 C、 D、6. 下列判断错误的是( )
A、 B、 C、 D、5. 《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺 .问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”. 就是说:圆堡瑽(圆柱体)的体积为 (底面圆的周长的平方 高),则由此可推得圆周率 的取值为( )A、 B、 C、 D、6. 下列判断错误的是( )
A、若随机变量 服从正态分布 ,则 ; B、若 组数据 的散点都在 上,则相关系数 ; C、若随机变量 服从二项分布: , 则 ; D、 是 的充分不必要条件;7. 执行如图所示的程序框图,若输入的 ,则输出的 , 的值分别为( ) A、 B、 C、 D、8. 已知定义在 上的函数 满足 ,且 是偶函数,当 时, .令 ,若在区间 内,函数 有4个不相等实根,则实数 的取值范围是( )A、 B、 C、 D、9. 我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有 架“歼— ”飞机准备着舰,如果乙机不能最先着舰,而丙机必须在甲机之前着舰(不一定相邻),那么不同的着舰方法种数为( )A、 B、 C、 D、10. 2017年中学数学信息技术研讨会,谈到了图像计算器在数学教学中的应用.如图输入曲线方程 ,计算器显示线段 ,则线段 的曲线方程为( )
A、 B、 C、 D、8. 已知定义在 上的函数 满足 ,且 是偶函数,当 时, .令 ,若在区间 内,函数 有4个不相等实根,则实数 的取值范围是( )A、 B、 C、 D、9. 我国的第一艘航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有 架“歼— ”飞机准备着舰,如果乙机不能最先着舰,而丙机必须在甲机之前着舰(不一定相邻),那么不同的着舰方法种数为( )A、 B、 C、 D、10. 2017年中学数学信息技术研讨会,谈到了图像计算器在数学教学中的应用.如图输入曲线方程 ,计算器显示线段 ,则线段 的曲线方程为( ) A、 B、 C、 D、11. 如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )
A、 B、 C、 D、11. 如图是某几何体的三视图,正视图是等边三角形,侧视图和俯视图为直角三角形,则该几何体外接球的表面积为( )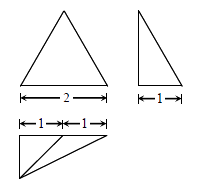 A、 B、 C、 D、12. 设函数 ,其中 ,若存在唯一的整数 ,使得 ,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、12. 设函数 ,其中 ,若存在唯一的整数 ,使得 ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 的展开式的常数项为 .
14. 将函数 的图象向右平移 个单位,得到函数 的图象,若 在 上为增函数,则 的最大值为 .
15. 已知直线 过点 ,若可行域 的外接圆直径为20,则 .
16. 给出以下四个命题,其中所有真命题的序号为 .①函数 在区间 上存在一个零点,则 的取值范围是 ;
②“ ”是“ 成等比数列”的必要不充分条件;
③ , ;
④若 ,则 .
三、解答题
-
17. 已知数列 是等差数列,数列 是公比大于零的等比数列,且 , .
(1)、求数列 和 的通项公式;
(2)、记 ,求数列 的前 项和 .18. 如图,在四棱锥 中,底面 为直角梯形, ,且 , 平面 . (1)、求 与平面 所成角的正弦值;(2)、棱 上是否存在一点 满足 ?若存在,求 的长;若不存在,说明理由.
(1)、求 与平面 所成角的正弦值;(2)、棱 上是否存在一点 满足 ?若存在,求 的长;若不存在,说明理由.
19. 心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取 名同学(男 人,女 人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
几何题
代数题
总计
男同学
22
8
30
女同学
8
12
20
总计
30
20
50
附表及公式:
 (1)、能否据此判断有 的把握认为视觉和空间能力与性别有关?(2)、现从选择做几何题的 名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为 ,求 的分布列和 .20. 已知椭圆 的左、右焦点分别为 短轴两个端点为 且四边形 是边长为 的正方形.
(1)、能否据此判断有 的把握认为视觉和空间能力与性别有关?(2)、现从选择做几何题的 名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为 ,求 的分布列和 .20. 已知椭圆 的左、右焦点分别为 短轴两个端点为 且四边形 是边长为 的正方形.(Ⅰ)求椭圆的方程;
(Ⅱ)若 分别是椭圆长轴的左、右端点,动点 满足 ,连接 ,交椭圆于点 .证明: 为定值.
