河南省2017-2018学年高三文数一轮复习诊断调研联考试卷
试卷更新日期:2018-03-16 类型:高考模拟
一、单选题
-
1. 集合 , ,则 中元素的个数为( )
A、0 B、1 C、2 D、32. 已知 ,复数 ,若 ,则 ( )A、 B、 C、 D、3. 某城市收集并整理了该市2017年1月份至10月份各月最低气温与最高气温(单位: )的数据,绘制了下面的折线图。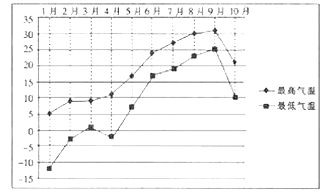
已知该市的各月最低气温与最高气温具有较好的线性关系,则根据该折线图,下列结论错误的是( )
A、最低气温与最高气温为正相关 B、10月的最高气温不低于5月的最高气温 C、月温差(最高气温减最低气温)的最大值出现在1月 D、最低气温低于 的月份有4个4. 在 中,角 , , 的对边分别为 , , ,若 , ,且 ,则 ( )
A、2 B、3 C、4 D、65. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有阳马,广五尺,袤七尺,高八尺,问积几何?”其意思为:“今有底面为矩形,一侧棱垂直于底面的四棱锥,它的底面长、宽分别为7尺和5尺,高为8尺,问它的体积是多少?”若以上的条件不变,则这个四棱锥的外接球的表面积为( )A、 平方尺 B、 平方尺 C、 平方尺 D、 平方尺6. 定义 表示不超过 的最大整数, ,例如 , ,执行如图所示的程序框图,若输入的 ,则输出的 ( ) A、 B、 C、 D、7. 若对于任意 都有 ,则函数 图象的对称中心为( )A、 ( ) B、 ( ) C、 ( ) D、 ( )8. 设 , 满足约束条件 若 取得最大值的最优解不唯一,则实数 的值为( )A、 或 B、 或 C、 或 D、 或29. 函数 的部分图象大致是( )A、
A、 B、 C、 D、7. 若对于任意 都有 ,则函数 图象的对称中心为( )A、 ( ) B、 ( ) C、 ( ) D、 ( )8. 设 , 满足约束条件 若 取得最大值的最优解不唯一,则实数 的值为( )A、 或 B、 或 C、 或 D、 或29. 函数 的部分图象大致是( )A、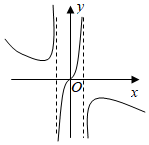 B、
B、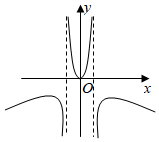 C、
C、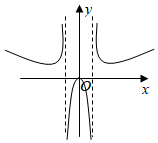 D、
D、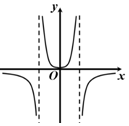 10. 已知某几何体的三视图如图所示,则该几何体的表面积为( )
10. 已知某几何体的三视图如图所示,则该几何体的表面积为( ) A、 B、 C、 D、11. 过抛物线 ( )的焦点 作斜率大于 的直线 交抛物线于 , 两点( 在 的上方),且 与准线交于点 ,若 ,则 ( )
A、 B、 C、 D、11. 过抛物线 ( )的焦点 作斜率大于 的直线 交抛物线于 , 两点( 在 的上方),且 与准线交于点 ,若 ,则 ( )
A、 B、 C、 D、12. 已知函数 与函数 的图象上存在关于 轴对称的点,则实数 的取值范围为( )
A、 B、 C、 D、二、填空题
-
13. 在 中, , ,则 .
14. 一只蜜蜂在一个正方体箱子里面自由飞行,若蜜蜂在飞行过程中始终保持在该正方体内切球范围内飞行,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为 .
15. 若 , ,则 .
16. 设 , 分别是双曲线 ( , )的左、右焦点,过 的直线 与双曲线分别交于 , ,且 在第一象限,若 为等边三角形,则双曲线的实轴长为 .
三、解答题
-
17. 已知等差数列 的公差不为零, ,且 , , 成等比数列.
(1)、求数列 的通项公式;
(2)、若 ,求数列 的前 项和 .18. 从某校高中男生中随机选取100名学生,将他们的体重(单位: )数据绘制成频率分布直方图,如图所示. (1)、估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);(2)、若要从体重在 , , 三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在 内的概率.19. 如图,在三棱台 中, , 分别是 , 的中点, , 平面 ,且 .
(1)、估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);(2)、若要从体重在 , , 三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在 内的概率.19. 如图,在三棱台 中, , 分别是 , 的中点, , 平面 ,且 . (1)、证明: 平面 ;(2)、若 , 为等边三角形,求四棱锥 的体积.20. 如图,椭圆 : ( )的焦距与椭圆 : 的短轴长相等,且 与 的长轴长相等,这两个椭圆在第一象限的交点为 ,直线 经过 在 轴正半轴上的顶点 且与直线 ( 为坐标原点)垂直, 与 的另一个交点为 , 与 交于 , 两点.
(1)、证明: 平面 ;(2)、若 , 为等边三角形,求四棱锥 的体积.20. 如图,椭圆 : ( )的焦距与椭圆 : 的短轴长相等,且 与 的长轴长相等,这两个椭圆在第一象限的交点为 ,直线 经过 在 轴正半轴上的顶点 且与直线 ( 为坐标原点)垂直, 与 的另一个交点为 , 与 交于 , 两点. (1)、求 的标准方程;(2)、求 .21. 已知函数 .(1)、若曲线 在 处的切线经过坐标原点,求 及该切线的方程;(2)、设 ,若函数 的值域为 ,求实数 的取值范围.
(1)、求 的标准方程;(2)、求 .21. 已知函数 .(1)、若曲线 在 处的切线经过坐标原点,求 及该切线的方程;(2)、设 ,若函数 的值域为 ,求实数 的取值范围.