河北省沧州市普通高中高三上学期理数教学质量监测试卷

试卷更新日期：2018-03-16 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | y = \sqrt{x}}$ ， $B = {x | \frac{1}{2} < 2^{x} < 4}$ ，则 $(∁_{R} A) \cap B =$ （）

A、 ${x | - 1 < x < 2}$ B、 ${x | - 1 < x < 0}$ C、 ${x | x < 1}$ D、 ${x | - 2 < x < 0}$

查看试题解析
2. 在区间 $[- 3, 2]$ 上随机选取一个数 $x$ ，则 $x \geq - 1$ 的概率为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
3. 下面关于复数 $z = \frac{2}{- 1 - i}$ 的四个命题：
$p_{1} : | z | = 2$
$p_{2} : z$ 的共轭复数 $\bar{z}$ 在复平面内对应的点的坐标为 $(- 1, - 1)$
$p_{3} : z$ 的虚部为-1
$p_{4} : z^{2} = - 2 i$
其中的真命题是（）

A、 $p_{2}, p_{3}$ B、 $p_{1}, p_{2}$ C、 $p_{2}, p_{4}$ D、 $p_{3}, p_{4}$

查看试题解析
4. 已知等差数列 ${a_{n}}$ ，且 $3 (a_{1} + a_{5}) + 2 (a_{6} + a_{9} + a_{12}) = 48$ ，则数列 ${a_{n}}$ 的前11项之和为（）

A、84 B、68 C、52 D、44

查看试题解析
5. 已知函数 $f (x)$ 是偶函数，且在 $[0, + \infty)$ 上是增函数，若 $f ({log}_{2} x) < f (1)$ ，则 $x$ 的取值范围是（）

A、 $(0, 2)$ B、 $(0, \frac{1}{2}) \cup (1, + \infty)$ C、 $(\frac{1}{2}, 2)$ D、 $(0, 1) \cup (2, + \infty)$

查看试题解析
6. 在 ${(x - \frac{1}{\sqrt{x}})}^{8}$ 的展开式中， $x^{5}$ 项的系数为（）

A、28 B、56 C、-28 D、-56

查看试题解析
7. 若 $cos α + 2 cos β = \sqrt{2}$ ， $sin α = 2 sin β - \sqrt{3}$ ， ${sin}^{2} (α + β) =$ （）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{4}$ D、0

查看试题解析
8. 阅读如图所示的程序框图，运行相应的程序，则输出 $S$ 的值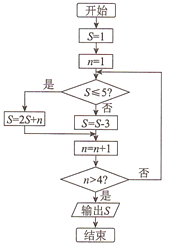为（）

A、5 B、11 C、14 D、19

查看试题解析
9. 如图，用虚线表示的网格的小正方形边长为1，实线表示某几何体的三视图，则此几何体的外接球半径为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
10. 已知 $4^{a} = 7$ ， $6^{b} = 8$ ，则 ${log}_{12} 21$ 可以用 $a, b$ 表示为（）

A、 $\frac{3 - b + 2 a b}{3 + b}$ B、 $\frac{2 a + b - a b}{3 + b}$ C、 $\frac{3 - b + 2 a b}{4 - 2 b}$ D、 $\frac{2 a + b - a b}{4 - 2 b}$

查看试题解析
11. 设 $F$ 为抛物线 $C : y^{2} = 4 x$ 的焦点，过点 $P (- 1, 0)$ 的直线 $l$ 交抛物线 $C$ 于 $A, B$ 两点，点 $Q$ 为线段 $A B$ 的中点，若 $| F Q | = 2 \sqrt{3}$ ，则 $| A B | =$ （）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
12. 已知数列 ${a_{n}}$ 满足 $a_{1} = 1$ ， $a_{n + 1} = 3 a_{n} + 2^{n} (n \in N^{*})$ ， $b_{n} = \frac{a_{n + 1}}{a_{n}}$ .设 $t \in Z$ ，若对于 $\forall n \in N^{*}$ ，都有 $b_{n} > t$ 恒成立，则 $t$ 的最大值为（）

A、3 B、4 C、7 D、9

查看试题解析

二、填空题

13. 已知单位向量 $\overset{⇀}{e_{1}}, \overset{⇀}{e_{2}}$ 的夹角为60°，则 $| \overset{⇀}{e_{1}} - 2 \overset{⇀}{e_{2}} | =$ ．

查看试题解析
14. 若 $x ， y$ 满足约束条件 ${\begin{matrix} x + 1 \geq 0 ， \\ x - y \leq 0 ， \\ x + y - 2 \leq 0 ， \end{matrix}$ 则 $\frac{y + 2}{x}$ 的取值范围为．

查看试题解析
15. 已知 $F_{1}, F_{2}$ 是双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 的两个焦点，点 $P$ 是双曲线 $C$ 上一点，若 $| P F_{1} | + | P F_{2} | = 4 a$ ，且 $| O P | = c$ ，则双曲线 $C$ 的离心率为．

查看试题解析
16. 如图，在 $Δ P A B$ 中， $P A = P B = 3 \sqrt{5}$ ， $A B = 6$ . $C ， D$ 分别是边 $P B ， P A$ 上的点，且 $C D ∥ A B$ .现将 $Δ P C D$ 沿直线 $C D$ 折起，形成四棱锥 $P - A B C D$ ，则此四棱锥的体积的最大值是．

查看试题解析

三、解答题

17. 已知函数 $f (x) = sin ω x cos ω x + \sqrt{3} {sin}^{2} ω x - \frac{\sqrt{3}}{2} (ω > 0)$ 的最小正周期为 $π$ ，将函数 $f (x)$ 的图象向左平移 $\frac{π}{6}$ 个单位长度，再向下平移 $\frac{1}{2}$ 个单位长度，得到函数 $y = g (x)$ 的图象.
（Ⅰ）求函数 $f (x)$ 的单调递增区间；
（Ⅱ）在锐角 $Δ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ .若 $g (\frac{A}{2}) = 0$ ， $a = 1$ ，求 $Δ A B C$ 面积的最大值.

查看试题解析
18. 如图所示，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $P A ⊥$ 平面 $A B C D$ ，且 $P A = A B = 1$ ，点 $E$ 在线段 $P C$ 上，且 $P E = 2 E C$ .
（Ⅰ）证明：平面 $B D E ⊥$ 平面 $P C D$ ；
（Ⅱ）求二面角 $P - B D - E$ 的余弦值.

查看试题解析
19. 某厂为检验车间一生产线是否工作正常，现从生产线中随机抽取一批零件样本，测量尺寸（单位： $mm$ ）绘成频率分布直方图如图所示：
（Ⅰ）求该批零件样本尺寸的平均数 $x$ 和样本方差 $s^{2}$ （同一组中的数据用该组区间的中点值作代表）；
（Ⅱ）若该批零件尺寸 $Z$ 服从正态分布 $N (μ ， σ^{2})$ ，其中 $μ$ 近似为样本平均数 $x$ ， $σ^{2}$ 近似为样本方差 $s^{2}$ ，利用该正态分布求 $P (54 < Z < 85.5)$ ；
（Ⅲ）若从生产线中任取一零件，测量尺寸为 $30 mm$ ，根据 $3 σ$ 原则判断该生产线是否正常？
附： $\sqrt{110} \approx 10.5$ ；若 $Z \sim N (μ ， σ^{2})$ ，则 $P (μ - σ < Z < μ + σ) = 0.6826$ ， $P (μ - 2 σ < Z < μ + 2 σ) = 0.9544$ ， $P (μ - 3 σ < Z < μ + 3 σ) = 0.9974$ .

查看试题解析
20. 对于椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，有如下性质：若点 $(x_{0}, y_{0})$ 是椭圆上的点，则椭圆在该点处的切线方程为 $\frac{x_{0} x}{a^{2}} + \frac{y_{0} y}{b^{2}} = 1$ .利用此结论解答下列问题.
（Ⅰ）求椭圆 $C$ 的标准方程；
（Ⅱ）若动点 $P$ 在直线 $x + y = 3$ 上，经过点 $P$ 的直线 $m, n$ 与椭圆 $C$ 相切，切点分别为 $M, N$ .求证直线 $M N$ 必经过一定点.

查看试题解析
21. 已知函数 $f (x) = ln x + \frac{a + 1}{x^{2}} + \frac{a - 1}{x}$ .
（Ⅰ）当 $a = - 1$ 时，求函数 $f (x)$ 在 $x = 1$ 处的切线方程；
（Ⅱ）试判断函数 $f (x)$ 零点的个数.

查看试题解析
22. 已知曲线 $C$ 的参数方程为 ${\begin{matrix} x = 2 c o s θ \\ y = s i n θ \end{matrix}$ （ $θ$ 为参数），直线 $l$ 的参数方程为 ${\begin{matrix} x = - 2 + \frac{\sqrt{2}}{2} t \\ y = 2 + \frac{\sqrt{2}}{2} t \end{matrix}$ （ $t$ 为参数）.
（Ⅰ）求曲线 $C$ 和直线 $l$ 的普通方程；
（Ⅱ）若点 $P$ 为曲线 $C$ 上一点，求点 $P$ 到直线 $l$ 的距离的最大值.

查看试题解析
23. 已知函数 $f (x) = | 2 x + 1 | - | x - a |$ .
（Ⅰ）当 $a = 4$ 时，求不等式 $f (x) > 2$ 的解集；
（Ⅱ）若 $f (x) \geq | x - 4 |$ 的解集包含 $[2 ， 3]$ ，求实数 $a$ 的取值范围.

查看试题解析