河北省沧州市普通高中2017-2018学年高三上学期文数教学质量监测试卷

试卷更新日期：2018-03-16 类型：期末考试

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ， $A = {x | x \leq 0}$ ， $B = {x | x \geq 1}$ ，则 $C_{U} (A \cup B) =$ （）

A、 ${x | x \geq 0}$ B、 ${x | x \leq 1}$ C、 ${x | 0 \leq x \leq 1}$ D、 ${x | 0 < x < 1}$

查看试题解析
2. 某校五人参加孔子学院志愿者选拔考试，已知这5人的平均考试成绩为91分，有2人得92分，1人得83分，1人得94分，由这5人得分所组成的一组数据的中位数是（）

A、91 B、92 C、93 D、94

查看试题解析
3. 已知 $(a + b i) (1 - 2 i) = 5$ （ $i$ 为虚数单位， $a, b \in R$ ），则 $a + b$ 的值为（）

A、-1 B、1 C、2 D、3

查看试题解析
4. 在区间 $[- 3, 2]$ 上随机选取一个数 $x$ ，则 $x \geq - 1$ 的概率为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
5. 双曲线 $\frac{x^{2}}{4} - y^{2} = 1$ 的右顶点到该双曲线的渐近线的距离为（）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{4 \sqrt{5}}{5}$ C、 $\frac{2 \sqrt{3}}{3}$ D、1

查看试题解析
6. 在空间中， $a, b$ 是两条不同的直线， $α ， β$ 是两个不同的平面，则下列命题中的真命题是（）

A、若 $a ∥ α$ ， $b ∥ α$ ，则 $a ∥ b$ B、若 $a \subset α$ ， $b \subset β$ ， $α ⊥ β$ ，则 $a ⊥ b$ C、若 $a ∥ α$ ， $a ∥ b$ ，则 $b ∥ α$ D、若 $α ∥ β$ ， $a \subset α$ 则 $a ∥ β$

查看试题解析
7. 已知 $f (x) = {\begin{matrix} 4^{x} - 1 ， x \geq 0 ， \\ f (x + 2) ， - 6 \leq x < 0 ， \end{matrix}$ 则方程 $f (x) = 3$ 的根的个数为（）

A、5 B、4 C、1 D、无数多个

查看试题解析
8. 已知变量 $x ， y$ 满足约束条件 ${\begin{matrix} x - y \geq 0 ， \\ x + y \leq 2 ， \\ y \geq 0 ， \end{matrix}$ 则 $z = 2 x + y$ 的最大值为（）

A、0 B、3 C、4 D、5

查看试题解析
9. 若函数 $f (x)$ 对任意的 $x \in R$ 恒有 $f (x + 1) = f (3 - x)$ ，且当 $x_{1}, x_{2} \in (2, + \infty)$ ， $x_{1} \neq x_{2}$ 时， $[f (x_{1}) - f (x_{2})] (x_{1} - x_{2}) > 0$ ，设 $a = f (0)$ ， $b = f (π)$ ， $c = f (1)$ ，则 $a, b, c$ 的大小关系为（）

A、 $c < b < a$ B、 $c < a < b$ C、 $b < c < a$ D、 $b < a < c$

查看试题解析
10. 阅读如图所示的程序框图，运行相应的程序，则输出 $S$ 的值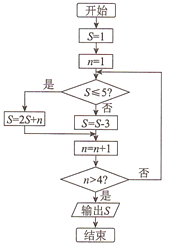为（）

A、5 B、11 C、14 D、19

查看试题解析
11. 已知点 $P$ 在以坐标原点为中心，坐标轴为对称轴，离心率为 $\frac{1}{2}$ 的椭圆上.若过点 $P$ 作长轴的垂线恰好过椭圆的一个焦点 $F_{1}$ ，与椭圆的另一交点为 $A$ .若 $Δ P F_{2} A$ 的面积为12（ $F_{2}$ 为椭圆的另一焦点），则椭圆的方程为（）

A、 $\frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$ B、 $\frac{x^{2}}{12} + \frac{y^{2}}{16} = 1$ C、 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 或 $\frac{x^{2}}{3} + \frac{y^{2}}{4} = 1$ D、 $\frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$ 或 $\frac{x^{2}}{12} + \frac{y^{2}}{16} = 1$

查看试题解析
12. 已知 $A, B, C$ 为 $Δ ABC$ 的三个内角，且 ${cos}^{2} (A - \frac{π}{6}) + {sin}^{2} (A + \frac{π}{6}) - 1 = \frac{\sqrt{3}}{2}$ ，若 $A, B, C$ 成等差数列， $b = \sqrt{3}$ ，则 $a =$ （）

A、 $\sqrt{6}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析

二、填空题

13. 设 $a = (1, 1)$ ， $b = (1, 2)$ ， $c = b + k a$ ，若 $a ⊥ c$ ,则 $k =$ ．

查看试题解析
14. 已知函数 $f (x) = x + \frac{a}{x} + b (x \neq 0)$ 在点 $(1 ， f (1))$ 处的切线方程为 $y = - 2 x + 5$ ，则 $a - b =$ ．

查看试题解析
15. 函数 $f (x) = 2 cos x sin (x + \frac{π}{3}) - \sqrt{3} {sin}^{2} x + sin x cos x$ 在 $x \in [- \frac{π}{4}, \frac{π}{6}]$ 时的最大值与最小值之和为．

查看试题解析
16. 已知三棱锥 $A - B C D$ ， $C D ⊥$ 面 $ABC$ ， $Rt Δ ABC$ 中两直角边 $A B = 5$ ， $B C = 3$ ，该三棱锥的外接球的表面积为 $50 π$ ，则三棱锥的体积为．

查看试题解析

三、解答题

17. 在等差数列 ${a_{n}}$ 中， $a_{1} + a_{6} = - 17$ ， $a_{2} + a_{7} = - 23$ .
（Ⅰ）求数列 ${a_{n}}$ 的通项公式；
（Ⅱ）设数列 ${2 a_{n} + b_{n}}$ 是首项为1，公比为 $q$ 的等比数列，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
18. 如图所示，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $P A ⊥$ 平面 $A B C D$ ，且 $P A = A B = 1$ ，点 $E$ 在线段 $P C$ 上，且 $P E = 2 E C$ .

（Ⅰ）证明：平面 $B D E ⊥$ 平面 $P C D$ ；
（Ⅱ）求四棱锥 $E - A B C D$ 的体积.

查看试题解析
19. 某化工厂为预测产品的回收率 $y$ ，需要研究它和原料有效成分含量 $x$ 之间的相关关系，现收集了4组对照数据。
$x$
3
4
5
6
$y$
2.5
3
4
4.5
（Ⅰ）请根据相关系数 $r$ 的大小判断回收率 $y$ 与 $x$ 之间是否存在高度线性相关关系；
（Ⅱ）请根据上表提供的数据，用最小二乘法求出 $y$ 关于 $x$ 的线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ ，并预测当 $x = 10$ 时回收率 $y$ 的值.
参考数据： $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \cdot \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$
$| r |$
1
0
$> 0.8$
$< 0.3$
其他
$x ， y$ 相关关系
完全相关
不相关
高度相关
低度相关
中度相关
$\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - b \bar{x}$

查看试题解析
20. 设抛物线 $C ： x^{2} = 2 p y (p > 0)$ 的焦点为 $F$ ，准线为 $l$ ，点 $A$ 在抛物线 $C$ 上，已知以点 $F$ 为圆心， $F A$ 为半径的圆 $F$ 交 $l$ 于 $B ， D$ 两点.
（Ⅰ）若 $B D = 2 p$ ， $Δ B D F$ 的面积为4，求抛物线 $C$ 的方程；
（Ⅱ）若 $A ， B ， F$ 三点在同一条直线 $m$ 上，直线 $n$ 与 $m$ 平行，且 $n$ 与抛物线 $C$ 只有一个公共点，求直线 $n$ 的方程.

查看试题解析
21. 已知函数 $f (x) = - a x^{3} + \frac{1}{2} x^{2} + 2 x - 1$ 在 $x = 1$ 处的切线斜率为2.
（Ⅰ）求 $f (x)$ 的单调区间和极值；
（Ⅱ）若 $f^{'} (x) - k ln x - 2 > 0$ 在 $[1 ， + \infty)$ 上无解，求 $k$ 的取值范围.

查看试题解析
22. 已知曲线 $C$ 的参数方程为 ${\begin{matrix} x = 2 c o s θ \\ y = s i n θ \end{matrix}$ （ $θ$ 为参数），直线 $l$ 的参数方程为 ${\begin{matrix} x = - 2 + \frac{\sqrt{2}}{2} t \\ y = 2 + \frac{\sqrt{2}}{2} t \end{matrix}$ （ $t$ 为参数）.
（Ⅰ）求曲线 $C$ 和直线 $l$ 的普通方程；
（Ⅱ）若点 $P$ 为曲线 $C$ 上一点，求点 $P$ 到直线 $l$ 的距离的最大值.

查看试题解析
23. 已知函数 $f (x) = | 2 x + 1 | - | x - a |$ .
（Ⅰ）当 $a = 4$ 时，求不等式 $f (x) > 2$ 的解集；
（Ⅱ）若 $f (x) \geq | x - 4 |$ 的解集包含 $[2 ， 3]$ ，求实数 $a$ 的取值范围.

查看试题解析

$\| r \|$	1	0	$> 0.8$	$< 0.3$	其他
$x ， y$ 相关关系	完全相关	不相关	高度相关	低度相关	中度相关

$x$	3	4	5	6
$y$	2.5	3	4	4.5