2016-2017学年四川省南充十中九年级上学期入学数学试卷
试卷更新日期:2016-11-17 类型:开学考试
一、选择题
-
1. 二次根式、、、、、中,最简二次根式有( )个.A、1个 B、2个 C、3个 D、4个2. 若式子 有意义,则x的取值范围为( )A、x≥2 B、x≠3 C、x≥2或x≠3 D、x≥2且x≠33. 如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A、7,24,25 B、3 ,4 ,5 C、3,4,5 D、4,7 ,84. 用配方法解一元二次方程x2+3x+1=0化解后的结果为( )A、(x+ )2= B、(x﹣ )2= C、(x+ )2=﹣ D、(x﹣ )2=﹣5. 如图,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=( )
 A、40° B、50° C、60° D、80°6. 下列函数是二次函数的是( )A、y=3x﹣4 B、y=ax2+bx+c C、y=(x+1)2﹣5 D、y=7. 如图所示,函数y1=|x|和 的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是( )
A、40° B、50° C、60° D、80°6. 下列函数是二次函数的是( )A、y=3x﹣4 B、y=ax2+bx+c C、y=(x+1)2﹣5 D、y=7. 如图所示,函数y1=|x|和 的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是( ) A、x<﹣1 B、﹣1<x<2 C、x>2 D、x<﹣1或x>28. 如果不为零的n是关于x的方程x2﹣mx+n=0的根,那么m﹣n的值为( )A、﹣ B、﹣1 C、 D、19. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
A、x<﹣1 B、﹣1<x<2 C、x>2 D、x<﹣1或x>28. 如果不为零的n是关于x的方程x2﹣mx+n=0的根,那么m﹣n的值为( )A、﹣ B、﹣1 C、 D、19. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )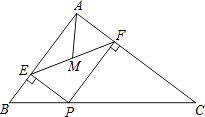 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. ﹣ + ﹣30﹣ = .11. 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1 , S2 , 则S1+S2的值为
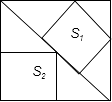 12. 平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=cm.13. 已知关于x的一元二次方程(a﹣1)x2+a2﹣1=0有一个根为0,则a=14. y=﹣2x2+8x﹣7的开口方向是 , 对称轴是 .15. 在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .16. 某一次函数的图象经过点(﹣1,3),且函数y随x的增大而减小,请你写出一个符合条件的函数解析式17. 某市2007年5月份某一周的日最高气温(单位:℃)分别为:25,28,30,29,31,32,28,这周的日最高气温的平均值是 .
12. 平行四边形ABCD的周长为20cm,对角线AC、BD相交于点O,若△BOC的周长比△AOB的周长大2cm,则CD=cm.13. 已知关于x的一元二次方程(a﹣1)x2+a2﹣1=0有一个根为0,则a=14. y=﹣2x2+8x﹣7的开口方向是 , 对称轴是 .15. 在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .16. 某一次函数的图象经过点(﹣1,3),且函数y随x的增大而减小,请你写出一个符合条件的函数解析式17. 某市2007年5月份某一周的日最高气温(单位:℃)分别为:25,28,30,29,31,32,28,这周的日最高气温的平均值是 .三、解答题
-
18. 解方程(1)、x2+4x+1=0(2)、(x﹣1)2+x=1(3)、3x2﹣2x﹣4=0(4)、x2﹣7x+12=0.19. 已知一元二次方程x2﹣6x+4=0的两根分别是a,b,求(1)、a2+b2(2)、(a-b)²的值.
20. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.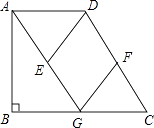 (1)、求证:四边形DEGF是平行四边形;(2)、当点G是BC的中点时,求证:四边形DEGF是菱形.21. 已知二次函数的图象经过点A(3,0),B(2,﹣3),C(0,﹣3),求函数的关系式.
(1)、求证:四边形DEGF是平行四边形;(2)、当点G是BC的中点时,求证:四边形DEGF是菱形.21. 已知二次函数的图象经过点A(3,0),B(2,﹣3),C(0,﹣3),求函数的关系式.
22.如图,在平面直角坐标系中一次函数 的图象分别交x、y轴于点A、B,与一次函数y=x的图象交于第一象限内的点C.
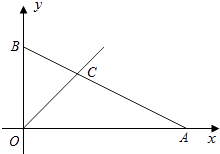 (1)、分别求出A、B、C、的坐标;(2)、求出△AOC的面积.23. 一次时装表演会预算中票价定为每张100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险5000(不列入成本费用),请解答下列问题:
(1)、分别求出A、B、C、的坐标;(2)、求出△AOC的面积.23. 一次时装表演会预算中票价定为每张100元,容纳观众人数不超过2000人,毛利润y(百元)关于观众人数x(百人)之间的函数图象如图所示,当观众人数超过1000人时,表演会组织者需向保险公司缴纳定额平安保险5000(不列入成本费用),请解答下列问题: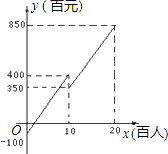 (1)、当观众不超过1000人时,毛利润y关于观众人数x的函数解析式和成本费用s(百元)关于观众人数x(百人)的函数解析式;(2)、若要使这次表演会获得36000元的毛利润,那么需售出多少张门票需支付成本费用多少元(当观众人数不超过1000人时,表演会的毛利润=门票收入﹣成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入﹣成本费用﹣平安保险费).24. 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)、当观众不超过1000人时,毛利润y关于观众人数x的函数解析式和成本费用s(百元)关于观众人数x(百人)的函数解析式;(2)、若要使这次表演会获得36000元的毛利润,那么需售出多少张门票需支付成本费用多少元(当观众人数不超过1000人时,表演会的毛利润=门票收入﹣成本费用;当观众人数超过1000人时,表演会的毛利润=门票收入﹣成本费用﹣平安保险费).24. 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.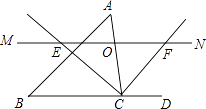 (1)、求证:OE=OF;(2)、若CE=12,CF=5,求OC的长;(3)、当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(1)、求证:OE=OF;(2)、若CE=12,CF=5,求OC的长;(3)、当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.