2015-2016学年辽宁省大连二十九中八年级上学期期中数学模拟试卷（1）
试卷更新日期：2016-11-17 类型：期中考试
一、选择题：
-
1. 下列计算结果正确的是（ ）A、b3•b3=2b3 B、（2x5）2=2x10 C、（﹣xy6）2=x2y12 D、x5•x2=x102. 下列轴对称图形中，对称轴条数最少的是（ ）A、等边三角形 B、正方形 C、正六边形 D、圆3. 如图，已知AB=AC，AD=AE，欲证△ABD≌△ACE，须补充的条件是（ ）
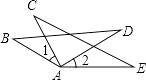A、∠B=∠C B、∠D=∠E C、∠1=∠2 D、∠CAD=∠DAC4. 下列说法中正确的是（ ）A、两个直角三角形全等 B、两个等腰三角形全等 C、两个等边三角形全等 D、两条直角边对应相等的直角三角形全等5. 如图所示，在△ABC中，点D是BC上一点，∠BAD=80°，AB=AD=DC，则∠C的大小为（ ）
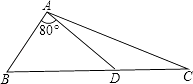A、50° B、40° C、20° D、25°6. 在△ABC与△DEF中，如果∠A=∠D，∠B=∠E，要使这两个三角形全等，还需要的条件可以是（ ）A、AB=EF B、BC=EF C、AB=AC D、∠C=∠D7. 如图，等腰△ABC中，AB=AC，P为其底角平分线的交点，将△BCP沿CP折叠，使B点恰好落在AC边上的点D处，若DA=DP，则∠A的度数为（ ）
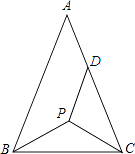A、20° B、30° C、32° D、36°二、填空题：
-
8. 等腰三角形的一个底角为30°，则顶角的度数是度．9. 若n边形的每个内角都等于150°，则n= ．10. ﹣（﹣2a2b）3=11. 已知：如图，Rt△ABC中，∠C=90°，沿过点B的一条直线BE折叠△ABC，使点C恰好落在AB边的中点D处，则∠A=度．
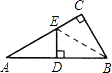12. 已知点A（3，3）和点B是平面内两点，且它们关于直线x=2轴对称，则点B的坐标为三、解答题：
-
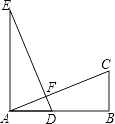
13. 已知，如图：AE⊥AB，BC⊥AB，AE=AB，ED=AC．求证：ED⊥AC．
四、解答题
-
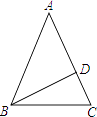
14. 已知：如图，AB=AC，BD⊥AC于D，请探究∠DBC与∠A的数量关系并说明理由．
15. 如图，已知AD为等腰三角形ABC的底角的平分线，∠C=90°，求证：AB=AC+CD．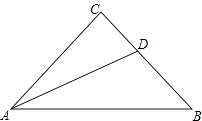
五、解答题
-
16. 如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连接BE，过C点作CF⊥BE，垂足为F．线段BF与图中现有的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．
结论：BF= ．
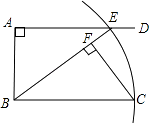17. 如图，在等边三角形ABC中，AB=6，点P是AB边上的任意一点（点P不与点A、点B重合），过点P作PD⊥AB，交直线BC于点D，作PE⊥AC，垂足为点F．
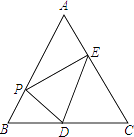(1)、求∠APE的度数；(2)、连接DE，当△PDE为等边三角形时，求BP的长．18. 已知：△ABC中，AB=AC，∠B=α．(1)、如图1，点D，E分别在边AB，AC上，线段DE的垂直平分线MN交直线BC于点M，交DE于点N，求证：BD+CE=BC．需补充条件∠EMN= （用含α的式子表示）补充条件后并证明；
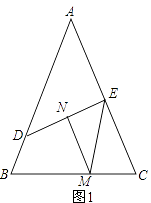(2)、把（1）中的条件改为点D，E分别在边BA、AC延长线上，线段DE的垂直平分线MN交直线BC于点M，交DE于点N（如图2），并补充条件∠EMN=（用含α的式子表示），通过观察或测量，猜想线段BD，CE与BC之间满足的数量关系，并予以证明．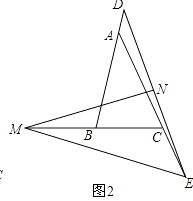
-