2016-2017学年福建省福州十八中九年级上学期开学数学试卷

试卷更新日期：2016-11-17 类型：开学考试

进入 出卷网 下载

一、选择题

  • 1. 一组数据1，2，3，4，5的方差是（  ）
    A、1 B、2 C、3 D、4

    查看试题解析

  • 2. 某地需要开辟一条隧道，隧道AB的长度无法直接测量．如图所示，在地面上取一点C，使点C均可直接到达A，B两点，测量找到AC和BC的中点D，E，测得DE的长为1100m，则隧道AB的长度为（  ）

    A、3300m B、2200m C、1100m D、550m

    查看试题解析

  • 3. 若平行四边形中两个内角的度数比为1：2，则其中较小的内角是（  ）
    A、90° B、60° C、120° D、45°

    查看试题解析

  • 4. 为了备战2016年里约奥运会，中国射击队正在积极训练．甲、乙两名运动员在相同的条件下，各射击10次．经过计算，甲、乙两人成绩的平均数均是9.5环，甲的成绩方差是0.125，乙的成绩的方差是0.85，那么这10次射击中，甲、乙成绩的稳定情况是（  ）
    A、甲较为稳定 B、乙较为稳定 C、两个人成绩一样稳定 D、不能确定

    查看试题解析

  • 5. 一次函数y=﹣2x+1的图象不经过下列哪个象限（　　）

    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 6. 已知一元二次方程x2﹣6x+c=0有一个根为2，则另一根为（  ）
    A、2 B、3 C、4 D、8

    查看试题解析

  • 7. 已知菱形的两条对角线的长分别是6和8，则菱形的周长是（  ）
    A、36 B、30 C、24 D、20

    查看试题解析

  • 8. 已知抛物线y=（a﹣5）x2﹣4x﹣1与x轴有交点，则a的取值范围是（  ）
    A、a≥1 B、a≠5 C、a＞1且a≠5 D、a≥1且a≠5

    查看试题解析

  • 9. 如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x≥ax+4的解集为（  ）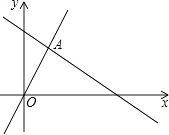

    A、x≥ 32 B、x≤3 C、x≤ 32 D、x≥3

    查看试题解析

  • 10.

    如图，正△ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→C的方向运动，到达点C时停止，设运动时间为x（秒），y=PC2 ， 则y关于x的函数的图象大致为（  ）

    A、 B、    C、 D、

    查看试题解析

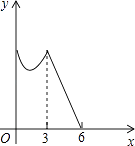
二、填空题

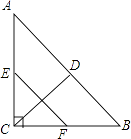
  • 11. 请写出一个图象经过第一、三象限的正比例函数的解析式 ．

    查看试题解析

  • 12. 方程x2﹣2x=0的根是 ．

    查看试题解析

  • 13. 某校规定学生的体育成绩由三部分组成；体育技能测试占50%，体育理论测试占20%，体育课外活动表现30%，甲同学的上述三部分成绩依次为96分，85分，90分，则甲同学的体育成绩为分．

    查看试题解析

  • 14. 如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若EF=8，则CD的长为 ．

    查看试题解析

  • 15. 将抛物线向左平移2个单位，再向下平移3个单位后，所得抛物线的解析式为y=x2﹣1，则原抛物线的解析式为 ．

    查看试题解析

  • 16.

    观察如图图形规律：当n=时，图形中“•”的个数是“△”的个数的一半．

    查看试题解析

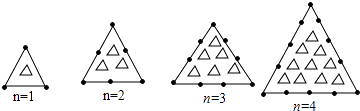
三、解答题

  • 17. 解方程：x2﹣4x+1=0

    查看试题解析

  • 18. 某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数：

    加工件数

    540

    450

    300

    240

    210

    120

    人数

    1

    1

    2

    6

    3

    2

    (1)、写出这15人该月加工零件数的平均数、中位数和众数．
    (2)、假如生产部负责人把每位工人的月加工零件数定为260（件），你认为这个定额是否合理，为什么？

    查看试题解析

  • 19. 如图，已知E、F分别是▱ABCD的边BC、AD上的点，且BE=DF．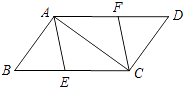

    (1)、求证：四边形AECF是平行四边形；
    (2)、若四边形AECF是菱形，且BC=10，∠BAC=90°，求BE的长．

    查看试题解析

  • 20. 某地区2013年投入教育经费2000万元，2015年投入教育经费2420万元．
    (1)、求2013年至2015年该地区投入教育经费的年平均增长率；
    (2)、根据（1）所得的年平均增长率，预计2016年该地区将投入教育经费多少万元．

    查看试题解析

  • 21. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．

    (1)、求直线AB的解析式；
    (2)、若直线AB上的点C在第一象限，且S△BOC=2，求点C的坐标．

    查看试题解析

  • 22.

    在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．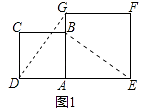

    (1)、小明发现DG=BE且DG⊥BE，请你给出证明．

    (2)、

    如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时△ADG的面积．

    查看试题解析

  • 23.

    如图，将矩形ABCD置于平面直角坐标系中，其中AD边在x轴上，AB=2，直线MN：y=x﹣4沿x轴的负方向以每秒1个单位的长度平移，设在平移过程中该直线被矩形ABCD的边截得的线段长度为m，平移时间为t，m与t的函数图象如图2所示．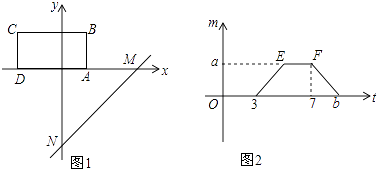

    (1)、点A的坐标为 ， 矩形ABCD的面积为；

    (2)、求a，b的值；

    (3)、在平移过程中，求直线MN扫过矩形ABCD的面积S与t的函数关系式，并写出自变量t的取值范围．

    查看试题解析

  • 24.

    如图，已知抛物线y=﹣x2+bx+9﹣b2（b为常数）经过坐标原点O，且与x轴交于另一点E．其顶点M在第一象限．

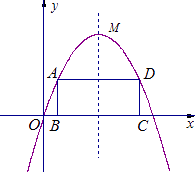    (1)、求该抛物线所对应的函数关系式；

    (2)、设点A是该抛物线上位于x轴上方，且在其对称轴左侧的一个动点；过点A作x轴的平行线交该抛物线于另一点D，再作AB⊥x轴于点B，DC⊥x轴于点C．

    ①当线段AB、BC的长都是整数个单位长度时，求矩形ABCD的周长；

    ②求矩形ABCD的周长的最大值，并写出此时点A的坐标；

    ③当矩形ABCD的周长取得最大值时，它的面积是否也同时取得最大值？请判断并说明理由．

    查看试题解析