2017-2018学年北师大版数学九年级下册同步训练：3.9 弧长及扇形的面积

试卷更新日期：2018-03-13 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，⊙O的半径为3，四边形ABCD内接于⊙O，连接OB、OD，若∠BOD=∠BCD，则 $\hat{B D}$ 的长为（）

A、π B、 $\frac{3}{2} π$ C、2π D、3π

查看试题解析
2. 如图，▱ABCD中，∠B=70°，BC=6，以AD为直径的⊙O交CD于点E，则 $\hat{D E}$ 的长为（）

A、 $\frac{1}{3}$ π B、 $\frac{2}{3}$ π C、 $\frac{7}{6}$ π D、 $\frac{4}{3}$ π

查看试题解析
3. 如图，⊙O是△ABC的外接圆，BC=2，∠BAC=30°，则劣弧 $\hat{B C}$ 的长等于（）

A、 $\frac{2 π}{3}$ B、 $\frac{π}{3}$ C、 $\frac{2 \sqrt{3} π}{3}$ D、 $\frac{\sqrt{3} π}{3}$

查看试题解析
4. 一个扇形的圆心角为60°，弧长为2π厘米，则这个扇形的半径为（）

A、6厘米 B、12厘米 C、 $2 \sqrt{3}$ 厘米 D、 $\sqrt{6}$ 厘米

查看试题解析
5. 如图，⊙O的半径为1，A，B，C是圆周上的三点，∠BAC=36°，则劣弧BC的长是（）

A、 $\frac{1}{5} π$ B、 $\frac{2}{5} π$ C、 $\frac{3}{5} π$ D、 $\frac{4}{5} π$

查看试题解析
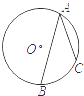6. 如图，正方形ABCD的边AB=1， $\hat{B D}$ 和 $\hat{A C}$ 都是以1为半径的圆弧，则无阴影两部分的面积之差是（）

A、 $\frac{π}{2} - 1$ B、1﹣ $\frac{π}{4}$ C、 $\frac{π}{3}$ ﹣1 D、1﹣ $\frac{π}{6}$

查看试题解析
7.
如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和为（　　）

A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
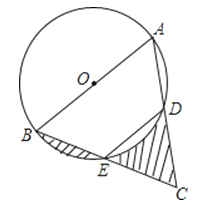8. 如图，将△ABC绕点C按顺时针旋转60°得到△A′B′C，已知AC=6，BC=4，则线段AB扫过的图形的面积为（）

A、 $\frac{2}{3}$ π B、 $\frac{8}{3}$ π C、6π D、 $\frac{10}{3}$ π

查看试题解析
9. 如图，某厂生产一种扇形折扇，OB=10cm，AB=20cm，其中裱花的部分是用纸糊的，若扇子完全打开摊平时纸面面积为 $\frac{1000}{3}$ π cm² ，则扇形圆心角的度数为（）

A、120° B、140° C、150° D、160°

查看试题解析
10. 如图，三个小正方形的边长都为1，则图中阴影部分面积的和是（）

A、 $\frac{π}{4}$ B、 $\frac{3 π}{8}$ C、 $\frac{π}{2}$ D、 $\frac{5 π}{8}$

查看试题解析

二、填空题

11. 如图，在△ABC中，∠ACB=90°，AC=1，AB=2，以点A为圆心、AC的长为半径画弧，交AB边于点D，则弧CD的长等于．（结果保留π）

查看试题解析
12. 如图，在扇形AOB中，AC为弦，∠AOB=130°，∠CAO=60°，半径=6，则 $\hat{B C}$ 的长为．

查看试题解析
13. 如图，在平面直角坐标系中，直线l的函数表达式为y=x，点O₁的坐标为（1，0），以O₁为圆心，O₁O为半径画圆，交直线l于点P₁ ，交x轴正半轴于点O₂ ，以O₂为圆心，O₂O为半径画圆，交直线l于点P₂ ，交x轴正半轴于点O₃ ，以O₃为圆心，O₃O为半径画圆，交直线l于点P₃ ，交x轴正半轴于点O₄；…按此做法进行下去，其中 $\hat{P_{2017} O_{2018}}$ 的长为．

查看试题解析
14. 如图，扇形纸叠扇完全打开后，扇形ABC的面积为300πcm² ， ∠BAC=120°，BD=2AD，则BD的长度为cm．

查看试题解析
15. 如图，⊙O的半径为2，点A，B在⊙O上，∠AOB=90°，则阴影部分的面积为．

查看试题解析
16. 如图，在圆心角为135°的扇形OAB中，半径OA=2cm，点C，D为 $\hat{A B}$ 的三等分点，连接OC，OD，AC，CD，BD，则图中阴影部分的面积为cm² ．

查看试题解析

三、解答题

17. 如图，点A、B、C在圆O上，AB为直径，且AB=4，AC=2．

(1)、求∠ABC的度数；

(2)、求弧AC的长度．

查看试题解析
18. 已知如图，在直角坐标系xOy中，点A，点B坐标分别为（﹣1，0），（0， $\sqrt{3}$ ），连结AB，OD由△AOB绕O点顺时针旋转60°而得．

(1)、求点C的坐标；

(2)、△AOB绕点O顺时针旋转60°所扫过的面积；

(3)、线段AB绕点O顺时针旋转60°所扫过的面积．

查看试题解析