2017-2018学年北师大版数学九年级下册同步训练：3.6.1 直线和圆的位置关系

试卷更新日期：2018-03-13 类型：同步测试

进入出卷网下载

一、选择题

1. 以坐标原点O为圆心，作半径为2的圆，若直线y=﹣x+b与⊙O相交，则b的取值范围是（）

A、0≤b＜2 $\sqrt{2}$ B、﹣2 $\sqrt{2} \leq b \leq 2 \sqrt{2}$ C、﹣2 $\sqrt{3} < b <$ 2 $\sqrt{3}$ D、﹣2 $\sqrt{2}$ ＜b＜2 $\sqrt{2}$

查看试题解析
2. 已知⊙O和直线L相交，圆心到直线L的距离为10cm，则⊙O的半径可能为（）

A、10cm B、6cm C、12cm D、以上都不对

查看试题解析
3. ⊙O的半径r=5cm，直线l到圆心O的距离d=4，则直线l与圆的位置关系（）

A、相离 B、相切 C、相交 D、重合

查看试题解析
4. 在平面直角坐标系xOy中，经过点（sin45°，cos30°）的直线，与以原点为圆心，2为半径的圆的位置关系是（）

A、相交 B、相切 C、相离 D、以上三者都有可能

查看试题解析
5. 如图，平面上⊙O与四条直线L₁、L₂、L₃、L₄的位置关系．若⊙O的半径为2cm，且O点到其中一条直线的距离为2.2cm，则这条直线是（）

A、L_l B、L₂ C、L₃ D、L4

查看试题解析
6. 已知等腰三角形的腰长为6cm，底边长为4cm，以等腰三角形的顶角的顶点为圆心5cm为半径画圆，那么该圆与底边的位置关系是（）

A、相离 B、相切 C、相交 D、不能确定

查看试题解析
7. 已知⊙O的半径为3，圆心O到直线L的距离为2，则直线L与⊙O的位置关系是（）

A、相交 B、相切 C、相离 D、不能确定

查看试题解析
8. 如图，AB是⊙O的直径，直线DA与⊙O相切于点A，DO交⊙O于点C，连接BC，若∠ABC=21°，则∠ADC的度数为（）

A、46° B、47° C、48° D、49°

查看试题解析
9. 如图，直线l是⊙O的切线，A为切点，B为直线l上一点，连接OB交⊙O于点C．若AB=12，OA=5，则BC的长为（）

A、5 B、6 C、7 D、8

查看试题解析
10. 如图，点A，B，C在⊙O上，∠ABC=29°，过点C作⊙O的切线交OA的延长线于点D，则∠D的大小为（）

A、29° B、32° C、42° D、58°

查看试题解析

二、填空题

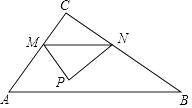
11. 如图，在Rt△ABC中，∠C=90°，AC≠BC，点M是边AC上的动点．过点M作MN∥AB交BC于N，现将△MNC沿MN折叠，得到△MNP．若点P在AB上．则以MN为直径的圆与直线AB的位置关系是．

查看试题解析
12. 若⊙O的半径为4cm，圆心O到直线l的距离为5cm，则直线l与⊙O的位置关系是．

查看试题解析
13. 已知点O到直线l的距离为6，以O为圆心，r为半径作⊙O，若⊙O上只有3个点到直线l的距离为2，则r的值为．

查看试题解析
14. 如图，BD是⊙O的切线，B为切点，连接DO与⊙O交于点C，AB为⊙O的直径，连接CA，若∠D=30°，⊙O的半径为4，则图中阴影部分的面积为．

查看试题解析
15. 如图，在直角坐标系中，⊙A的圆心A的坐标为（﹣1，0），半径为1，点P为直线y=﹣ $\frac{3}{4}$ x+3上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是．

查看试题解析
16. 如图，AB与⊙O相切于点B，线段OA与弦BC垂直，垂足为D，AB=BC=2，则∠AOB=°．

查看试题解析

三、解答题

17. 如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D的切线分别交AB，AC的延长线于E，F，连接BD．

(1)、求证：AF⊥EF；

(2)、若AC=6，CF=2，求⊙O的半径．

查看试题解析
18. 已知AB是⊙O的直径，AT是⊙O的切线，∠ABT=50°，BT交⊙O于点C，E是AB上一点，延长CE交⊙O于点D．

(1)、如图①，求∠T和∠CDB的大小；

(2)、如图②，当BE=BC时，求∠CDO的大小．

查看试题解析