2017-2018学年北师大版数学九年级下册同步训练：3.5 确定圆的条件
试卷更新日期：2018-03-13 类型：同步测试
一、选择题
-
1. 下列说法中正确的是（ ）A、不在同一条直线上的三个点确定一个圆 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、在同圆或等圆中，相等的弦所对的圆周角相等2. 下列说法中，正确的是（ ）A、三点确定一个圆 B、三角形有且只有一个外接圆 C、四边形都有一个外接圆 D、圆有且只有一个内接三角形3.
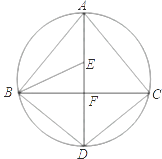
小明不慎把家里的圆形镜子打碎了，其中四块碎片如图所示，为了配到与原来大小一样的圆形镜子，小明带到商店去的一块碎片应该是（ ）
A、第一块 B、第二块 C、第三块 D、第四块4.如图，已知点平面直角坐标系内三点A（3，0）、B（5，0）、C（0，4），⊙P经过点A、B、C，则点P的坐标为（ ）
A、（6，8） B、（4，5） C、（4，） D、（4，）5. 如图，点D，E分别是⊙O的内接正三角形ABC的AB，AC边上的中点，若⊙O的半径为2，则DE的长等于（ ）
A、 B、 C、1 D、6. 如图，O为锐角三角形ABC的外心，四边形OCDE为正方形，其中E点在△ABC的外部，判断下列叙述何者正确（ ）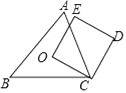
A、O是△AEB的外心，O是△AED的外心 B、O是△AEB的外心，O不是△AED的外心 C、O不是△AEB的外心，O是△AED的外心 D、O不是△AEB的外心，O不是△AED的外心7. 如图，△ABC是⊙O的内接三角形，∠C=30°，⊙O的半径为5，若点P是⊙O上的一点，在△ABP中，PB=AB，则PA的长为（ ）
A、5 B、 C、5 D、58. 如图，⊙O的半径为6，△ABC是⊙O的内接三角形，连接OB，OC，若∠BAC与∠BOC互补，则线段BC的长为（ ）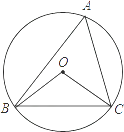
A、 B、3 C、 D、69. 如图，在平面直角坐标系xOy中，点A为（0，3），点B为（2，1），点C为（2，﹣3）．则经画图操作可知：△ABC的外心坐标应是（ ）
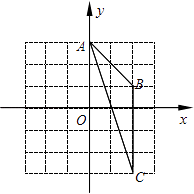A、（0，0） B、（1，0） C、（﹣2，﹣1） D、（2，0）10. 如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，∠C=50°，∠ABC的平分线BD交⊙O于点D，则∠BAD的度数是（ ）
A、95° B、90° C、85° D、75°二、填空题
-
11. 如图，点 A，B，C均在6×6的正方形网格格点上，过A，B，C三点的外接圆除经过A，B，C三点外还能经过的格点数为 ．
12. 当点A（1，2），B（3，﹣3），C（m，n）三点可以确定一个圆时，m，n需要满足的条件 ．13. 下列说法：①直径是弦；②经过三点一定可以作圆；③三角形的外心到三角形各顶点的距离相等；④长度相等的弧是等弧；⑤平分弦的直径垂直于弦．其中正确的是 （填序号）．14. 如图，在平面直角坐标系xOy中，点A、B、P的坐标分别为（1，0），（2，5），（4，2）．若点C在第一象限内，且横坐标、纵坐标均为整数，P是△ABC的外心，则点C的坐标为 ．
15. 在Rt△ABC中，∠ACB=90°，在斜边AB上分别截取AD=AC，BE=BC，DE=6，点O是△CDE的内心，如图所示，则点O到△ABC的三边的距离之和是 ．
16. 如图，AD是△ABC的高，AE是△ABC的外接圆⊙O的直径，且AB=6，AC=5，AD=3，则⊙O的直径AE= ．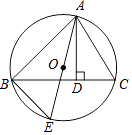
三、解答题
