2017-2018学年北师大版数学九年级下册同步训练：3.4.2 圆周角和圆心角的关系
试卷更新日期：2018-03-13 类型：同步测试
一、选择题
-
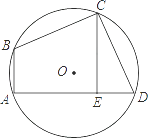
1. 如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC于D，交BC于E，连接AE，则下列结论中不一定正确的是（ ）
A、AE⊥BC B、BE=EC C、ED=EC D、∠BAC=∠EDC2. 如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点．下列四个角中，一定与∠ACD互余的角是（ ）
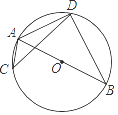A、∠ADC B、∠ABD C、∠BAC D、∠BAD3. 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED=20°，则∠BCD的度数为（ ）
A、100° B、110° C、115° D、120°4. 如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD=30°，则∠BAD为（ ）
A、30° B、50° C、60° D、70°5. 如图，AB是⊙O的直径，CD是⊙O的弦，若∠BAD=48°，则∠DCA的大小为（ ）
A、48° B、42° C、45° D、24°6. 如图，BD是⊙O的直径，∠A=60°，则∠DBC的度数是（ ）
A、30° B、45° C、60° D、25°7. 如图，AB是半圆的直径，点D是弧AC的中点，∠ABC=50°，则∠DAB等于（ ）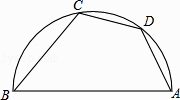
A、60° B、65° C、70° D、75°8. 如图，四边形ABCD内接于⊙O，AB经过圆心，∠B=3∠BAC，则∠ADC等于（ ）
A、100° B、112.5° C、120° D、135°9. 如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（ ）
A、 B、 C、 D、10. 如图，四边形ABCD为⊙O的内接四边形．延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC=50°，则∠DBC的度数为（ ）
A、50° B、60° C、80° D、90°二、填空题
-
11. 如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD的度数是 ．
12. 如图，AB为⊙O的直径，C、D为⊙O上的点， = ．若∠CAB=40°，则∠CAD= ．
13. 如图，△ABC内接于⊙O，∠ACB=90°，∠ACB的角平分线交⊙O于D．若AC=6，BD=5 ，则BC的长为 ．
14. 如图，A、B、C是⊙O上的三点，且四边形OABC是菱形．若点D是圆上异于A、B、C的另一点，则∠ADC的度数是 ．
15. 如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4：3：5，则∠D的度数是°．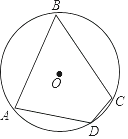
16. 如图，四边形ABCD是⊙O的内接四边形，点D是 的中点，点E是 上的一点，若∠CED=40°，则∠ADC=度．
三、解答题
