2017-2018学年北师大版数学八年级下册同步训练：3.2 图形的旋转 课时1
试卷更新日期：2018-03-13 类型：同步测试
一、知识点1旋转及相关概念
-
1. 在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动叫做,这个定点叫做,转动的角叫做角.
2. 如图，△AOB绕着点O旋转至△A'OB'的位置，此时：
(1)、点B的对应点是；
(2)、旋转中心是 ， 旋转角为；
(3)、∠A的对应角是 ， 线段OB的对应线段是线段.
3. 将数字“6”旋转180°，得到数字“9”，将数字“9”旋转180°，得到数字“6”，现将数字“69”旋转180°，得到的数字是（ ）A、96 B、69 C、66 D、994. 如图，在平面直角坐标系中，点B，C，E在y轴上，Rt△ABC经过变换得到Rt△ODE，若点C的坐标为(0，1)，AC=2，则这种变换可以是（ ）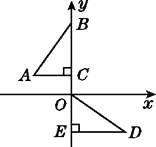
A、△ABC绕点C顺时针旋转90°，再向下平移3个单位长度 B、△ABC绕点C顺时针旋转90°，再向下平移1个单位长度 C、△ABC绕点C逆时针旋转90°，再向下平移1个单位长度 D、△ABC绕点C逆时针旋转90°，再向下平移3个单位长度5. 在△ABC中，∠BAC=33°，将△ABC绕点A按顺时针方向旋转50°，对应得到△AB'C'，则∠B'AC=.
二、知识点2旋转的性质
-
6. 旋转的性质:
(1)、对应点到旋转中心的距离;
(2)、任意一组对应点与旋转中心的连线所成的角等于;
(3)、旋转前、后的图形.
7. 如图，在平面直角坐标系xOy中，△A'B'C'由△ABC绕点P旋转得到，则点P的坐标为（ ）
A、(0，1) B、(1，-1) C、(0，-1) D、(1，0)8. 如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则B、D两点间的距离为（ ）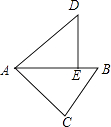
A、 B、2 C、3 D、29. 如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A1B1C，当点A1落在AB边上时，连接B1B，取BB1的中点D，连接A1D，则A1D的长度是（ ）
A、 B、2 C、3 D、2三、培优检测
-
10. 如图，在Rt△ABC中，∠ACB=90°，点D，E分别在AB，AC上，CE=BC，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CF，连接EF.
(1)、补充完成图形；(2)、若EF∥CD，求证：∠BDC=90°.
11. 如图，P为等边三角形ABC内部一点，△ABP旋转后能与△CBP'重合.
(1)、旋转中心是哪一点?旋转角是多少度?(2)、连接PP'，△BPP'是什么三角形?并说明你的理由.
12. 问题：如图①，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，试判断BE，EF，FD之间的数量关系.
(1)、【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG的位置，从而发现EF=BE+FD，请你利用图①证明上述结论.
(2)、【类比引申】如图②，在四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E，F分别在边BC，CD上，则当∠EAF与∠BAD满足关系时，仍有EF=BE+FD.请说明理由.
(3)、【探究应用】如图③，在某公园的同一水平面上，四条通道围成四边形ABCD.已知AB=AD=80 m，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC，CD上分别有景点E，F，且AE⊥AD，DF=40( -1)m，现要在E，F之间修一条笔直的道路，求这条道路EF的长(结果精确到1 m，参考数据： ≈1.41， ≈1.73).