2017-2018学年北师大版数学七年级下册同步训练：4.3.2 探索三角形全等的条件 asa aas
试卷更新日期：2018-03-12 类型：同步测试
一、选择——基础知识运用
-
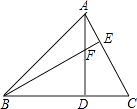
1. 在△ABC和△EMN中，已知∠A=50°，∠B=60°，∠E=70°，∠M=60°，AC=EN，则这两个三角形（ ）A、一定全等 B、一定不全等 C、不一定全等 D、以上都不对2. 如图，∠B=∠C，增加哪个条件可以让△ABD≌△ACE？（ ）
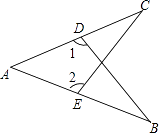A、BD=AD B、AB=AC C、∠1=∠2 D、以上答案都不对3.如图所示，∠E=∠F，∠B=∠C，AE=AF，以下结论：①∠FAN=∠EAM；②EM=FN；③△ACN≌△ABM；④CD=DN．其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个4. 如图，∠BAC=90°，BD⊥DE，CE⊥DE，添加下列条件后仍不能使△ABD≌△CAE的条件是（ ）
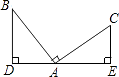A、AD=AE B、AB=AC C、BD=AE D、AD=CE5. 如图，AC平分∠BAD，∠B=∠D，AB=8cm，则AD=（ ）
A、6cm B、8cm C、10cm D、4cm二、解答——知识提高运用
-
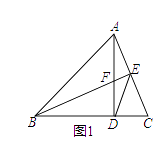
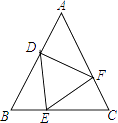
6. 已知，如图，△ABC中，AB=AC，动点D、E、F在AB、BC、AC上移动，移动过程中始终保持BD=CE，∠DEF=∠B，请你分析是否存在始终与△BDE全等的三角形，并说明理由。
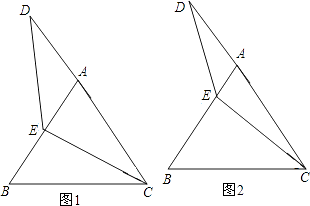
7. 如图，AB=AD，∠BAD=∠EAC，∠C=∠E，求证：AE=AC。
8. 如图，已知，在四边形ABCD中，E是AC上一点，∠DAC=∠BAC，∠DCA=∠BCA．求证：∠DEC=∠BEC。
