2018年高考数学提分专练：第4题逻辑用语（选择题）

试卷更新日期：2018-03-12 类型：二轮复习

进入出卷网下载

一、真题演练

1. 设有下面四个命题
p₁：若复数z满足 $\frac{1}{z}$ ∈R，则z∈R；
p₂：若复数z满足z²∈R，则z∈R；
p₃：若复数z₁ ， z₂满足z₁z₂∈R，则z₁= $\bar{z_{2}}$ ；
p₄：若复数z∈R，则 $\bar{z}$ ∈R．
其中的真命题为（　　）

A、p₁ ， p₃ B、p₁ ， p₄ C、p₂ ， p₃ D、p₂ ， p₄

查看试题解析
2.
某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．
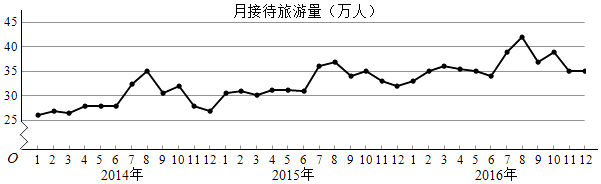
根据该折线图，下列结论错误的是（）

A、月接待游客量逐月增加 B、年接待游客量逐年增加 C、各年的月接待游客量高峰期大致在7，8月 D、各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

查看试题解析

二、模拟实训

3. 已知条件p：k= $\sqrt{3}$ ；条件q：直线y=kx+2与圆x²+y²=1相切，则￢p是￢q的（）

A、充分必要条件 B、必要不充分条件 C、充分不必要条件 D、既不充分也不必要条件

查看试题解析
4. 已知：
命题p：若函数f（x）=x²+|x﹣a|是偶函数，则a=0．
命题q：∀m∈（0，+∞），关于x的方程mx²﹣2x+1=0有解．
在①p∨q；②p∧q；③（￢p）∧q；④（￢p）∨（￢q）中为真命题的是（）

A、②③ B、②④ C、③④ D、①④

查看试题解析
5. 命题“ $\exists x_{0} \in R, x_{0}^{2} - x_{0} - 1 > 0$ ”的否定是（）

A、 $\forall x \in R, x_{}^{2} - x - 1 \leq 0$ B、 $\forall x \in R, x_{}^{2} - x - 1 > 0$ C、 $\exists x_{0} \in R, x_{0}^{2} - x_{0} - 1 \leq 0$ D、 $\exists x_{0} \in R, x_{0}^{2} - x_{0} - 1 \geq 0$

查看试题解析
6. “抛物线 $y = a x^{2}$ 的准线方程为 $y = 2$ ”是“抛物线 $y = a x^{2}$ 的焦点与双曲线 $\frac{y^{2}}{3} - x^{2} = 1$ 的焦点重合”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
7. 已知非零平面向量 $\vec{a}$ ， $\vec{b}$ ，则“| $\vec{a} + \vec{b}$ |=| $\vec{a}$ |+| $\vec{b}$ |”是“存在非零实数λ，使 $\vec{b}$ =λ $\vec{a}$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
8. 下列命题中正确命题的个数是（）
①对于命题p：∃x∈R，使得x²+x+1＜0，则￢p：∀x∈R，均有x²+x+1＞0；
②命题“已知x，y∈R，若x+y≠3，则x≠2或y≠1”是真命题；
③回归直线的斜率的估计值为1.23，样本点的中心为（4，5），则回归直线方程为 $\hat{y}$ =1.23x+0.08；
④m=3是直线（m+3）x+my﹣2=0与直线mx﹣6y+5=0互相垂直的充要条件．

A、1 B、3 C、2 D、4

查看试题解析
9. 命题p：sin2x=1，命题q：tanx=1，则p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
10. 在射击训练中，某战士射击了两次，设命题p是“第一次射击击中目标”，命题q是“第二次射击击中目标”，则命题“两次射击中至少有一次没有击中目标“为真命题的充要条件是（）

A、（￢p）∨（￢q）为真命题 B、p∨（￢q）为真命题 C、（￢p）∧（￢q）为真命题 D、p∨q为真命题

查看试题解析
11. “m≤﹣ $\frac{1}{2}$ ”是“∀x＞0，使得 $\frac{x}{2}$ + $\frac{1}{2 x}$ ﹣ $\frac{3}{2}$ ＞m是真命题”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
12. 在一次抛硬币实验中，甲、乙两人各抛一枚硬币一次，设命题p是“甲抛的硬币正面向上”，q是“乙抛的硬币正面向上”，则命题“至少有一人抛的硬币是正面向下”可表示为（）

A、（￢p）∨（￢q） B、p∧（￢q） C、（￢p）∧（￢q） D、p∨q

查看试题解析
13. 下列命题中，真命题的个数为①对任意的a，b∈R，a＞b是a|a|＞b|b|的充要条件；②在△ABC中，若A＞B，则sinA＞sinB；③非零向量 $\vec{a} ， \vec{b}$ ，若 $\vec{a} \cdot \vec{b} > 0$ ，则向量 $\vec{a}$ 与向量 $\vec{b}$ 的夹角为锐角；④ $\frac{l n 3}{3} > \frac{l n 2}{2} > \frac{l n 5}{5}$ ．（）

A、1 B、2 C、3 D、4

查看试题解析
14. “a＞1“是“ $\frac{1}{a}$ ＜1“的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、非充分非必要条件

查看试题解析
15. “ $0 < a < 1$ ”是“ $a x^{2} + 2 a x + 1 > 0$ 的解集是实数集R”的（）

A、充分而非必要条件 B、必要而非充分条件 C、充要条件 D、既非充分也非必要条件

查看试题解析
16. 命题p：若a＞b，则|a|＞|b|；命题q：当a=0时，f（x）=xln（x+a）²为奇函数，则下列命题中为真命题的是（　　）

A、（￢p）∨q B、p∨（￢q） C、p∧q D、（￢p）∧（￢q）

查看试题解析
17. 已知命题p：“存在x₀∈[1，+∞），使得（log₂3） $^{x_{0}}$ ≥1”，则下列说法正确的是（　　）

A、p是假命题；￢p“任意x∈[1，+∞），都有（log₂3）^x＜1” B、p是真命题；￢p“不存在x₀∈[1，+∞），使得（log₂3） $^{x_{0}}$ ＜1” C、p是真命题；￢p“任意x∈[1，+∞），都有（log₂3）^x＜1” D、p是假命题；￢p“任意x∈（﹣∞，1），都有（log₂3）^x＜1”

查看试题解析
18. 已知命题p：∀x∈（1，+∞），x³+16＞8x，则命题p的否定为（）

A、￢p：∀x∈（1，+∞），x³+16≤8x B、￢p：∀x∈（1，+∞），x³+16＜8x C、￢p：∃x₀∈（1，+∞），x₀³+16≤8x₀ D、￢p：∃x₀∈（1，+∞），x₀³+16＜8x₀

查看试题解析
19. 设m、n是两条不同的直线，α、β是两个不同的平面，则m⊥β的一个充分条件是（）

A、α⊥β且m⊂α B、m∥n且n⊥β C、α⊥β且m∥α D、m⊥n且n∥β

查看试题解析
20. “ $\frac{1}{a}$ ＞1”是“a＜1”的（）

A、充分条件但不是必要条件 B、必要条件但不是充分条件 C、充要条件 D、既不是充分条件，也不是必要条件

查看试题解析

2018年高考数学提分专练：第4题 逻辑用语（选择题）

一、真题演练

二、模拟实训

2018年高考数学提分专练：第4题逻辑用语（选择题）