2018年高考数学提分专练:第3题 概率(选择题)
试卷更新日期:2018-03-12 类型:二轮复习
一、真题演练
-
1. 从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )A、 B、 C、 D、2.
如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )
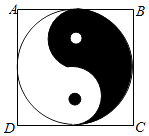 A、 B、 C、 D、
A、 B、 C、 D、二、模拟实训
-
3. 七巧板是我们祖先的一项创造,被誉为“东方魔板”,它是由五块等腰直角三角形(两块全等的小三角形、一块中三角形和两块全等的大三角形)、一块正方形和一块平行四边形组成的.如图是一个用七巧板拼成的正方形中任取一点,则此点取自黑色部分的概率是( )
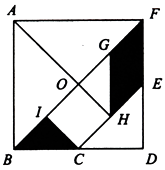 A、 B、 C、 D、4. 五个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )
A、 B、 C、 D、4. 五个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )
A、 B、 C、 D、5. 有5道题中,有3道理科题和2道文科题,如果不放回地依次抽取2道题,则在第1次抽到理科题的条件下,第2次抽到理科题的概率为( )A、 B、 C、 D、6. 小李去上班可以搭同事的顺风车,同事经过小李家门口的时间是8:00且只等小李5分钟,小李在7:55到8:20到家门口,小李可以搭上顺风车的概率是( )A、 B、 C、 D、7. 现有4张卡片,正面分别标有1,2,3,4,背面完全相同.将卡片洗匀,背面向上放置,甲、乙二人轮流抽取卡片,每人每次抽取一张,抽取后不放回,甲先抽.若二人约定,先抽到标有偶数的卡片者获胜,则甲获胜的概率是( )A、 B、 C、 D、8. 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( ) A、 B、 C、 D、9. 一袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为( )A、 B、 C、 D、10. 连续投掷两次骰子得到的点数分别为m,n,向量 与向量 的夹角记为α,则α 的概率为( )A、 B、 C、 D、11. 某路口的红绿灯,红灯时间为30秒,黄灯时间为5秒,绿灯时间为40秒,假设你在任何时间到达该路口是等可能的,则当你到达该路口时,看见不是黄灯的概率是( )A、 B、 C、. D、12. 假设你和同桌玩数字游戏,两人各自在心中想一个整数,分别记为x,y,且x,y∈[1,4].如果满足|x﹣y|≤1,那么就称你和同桌“心灵感应”,则你和同桌“心灵感应”的概率为( )A、 B、 C、 D、13. 设甲、乙两人每次射击命中目标的概率分别为 ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )A、 B、 C、 D、14. 三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实,黄实,利用2×勾×股+(股﹣勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2 , 设勾股中勾股比为1: ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
A、 B、 C、 D、9. 一袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为( )A、 B、 C、 D、10. 连续投掷两次骰子得到的点数分别为m,n,向量 与向量 的夹角记为α,则α 的概率为( )A、 B、 C、 D、11. 某路口的红绿灯,红灯时间为30秒,黄灯时间为5秒,绿灯时间为40秒,假设你在任何时间到达该路口是等可能的,则当你到达该路口时,看见不是黄灯的概率是( )A、 B、 C、. D、12. 假设你和同桌玩数字游戏,两人各自在心中想一个整数,分别记为x,y,且x,y∈[1,4].如果满足|x﹣y|≤1,那么就称你和同桌“心灵感应”,则你和同桌“心灵感应”的概率为( )A、 B、 C、 D、13. 设甲、乙两人每次射击命中目标的概率分别为 ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )A、 B、 C、 D、14. 三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明,下面是赵爽的弦图及注文,弦图是一个以勾股形之弦为边的正方形,其面积称为弦实,图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实,黄实,利用2×勾×股+(股﹣勾)2=4×朱实+黄实=弦实,化简,得勾2+股2=弦2 , 设勾股中勾股比为1: ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )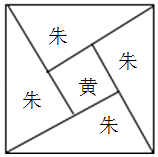 A、866 B、500 C、300 D、13415. 现从甲、乙两个品牌共9个不同的空气净化器中选出3个分别测试A、B、C三项指标,若取出的3个空气净化器中既有甲品牌又有乙品牌的概率为 ,那么9个空气净化器中甲、乙品牌个数分布可能是( )A、甲品牌1个,乙品牌8个 B、甲品牌2个,乙品牌7个 C、甲品牌3个,乙品牌6个 D、甲品牌4个,乙品牌5个
A、866 B、500 C、300 D、13415. 现从甲、乙两个品牌共9个不同的空气净化器中选出3个分别测试A、B、C三项指标,若取出的3个空气净化器中既有甲品牌又有乙品牌的概率为 ,那么9个空气净化器中甲、乙品牌个数分布可能是( )A、甲品牌1个,乙品牌8个 B、甲品牌2个,乙品牌7个 C、甲品牌3个,乙品牌6个 D、甲品牌4个,乙品牌5个