2017-2018学年北师大版数学九年级下册同步训练：2.4.1 二次函数的应用

试卷更新日期：2018-03-09 类型：同步测试

进入出卷网下载

一、选择题

1. 足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如下表：
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论：①足球距离地面的最大高度为20m；②足球飞行路线的对称轴是直线t= $\frac{9}{2}$ ；③足球被踢出9s时落地；④足球被踢出1.5s时，距离地面的高度是11m．其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 烟花厂为雁荡山旅游节特别设计制作一种新型礼炮，这种礼炮的升空高度h（m）与飞行时间t（s）的关系式是h=﹣ $\frac{5}{2}$ t²+20t+1，若这种礼炮在点火升空到最高点处引爆，则从点火升空到引爆需要的时间为（）

A、3s B、4s C、5s D、6s

查看试题解析
3. 一位篮球运动员跳起投篮，篮球运行的高度y（米）关于篮球运动的水平距离x（米）的函数解析式是y=﹣ $\frac{1}{5}$ （x﹣2.5）²+3.5．已知篮圈中心到地面的距离3.05米，如果篮球运行高度达到最高点之后能准确投入篮圈，那么篮球运行的水平距离为（）

A、1米 B、2米 C、4米 D、5米

查看试题解析
4. 为搞好环保，某公司准备修建一个长方体的污水处理池，池底矩形的周长为100m，则池底的最大面积是（）

A、600 m² B、625 m² C、650 m² D、675 m²

查看试题解析
5. 如图，铅球运动员掷铅球的高度y（m）与水平距离x（m）之间的函数关系式是y=﹣ $\frac{1}{12}$ x²+ $\frac{2}{3}$ x+ $\frac{5}{3}$ ，则该运动员此次掷铅球的成绩是（）

A、6m B、12m C、8m D、10m

查看试题解析
6. 如图，一场篮球赛中，篮球运动员跳起投篮，已知球出手时离地面高2.2m，与篮圈中心的水平距离为8m，当球出手后水平距离为4m时达到最大高度4m，篮圈运行的轨迹为抛物线的一部分，篮圈中心距离地面3m，运动员发现未投中，若假设出手的角度和力度都不变，要使此球恰好通过篮圈中心，运动员应该跳得（）

A、比开始高0.8m B、比开始高0.4m C、比开始低0.8m D、比开始低0.4m

查看试题解析
7. 一个网球发射器向空中发射网球，网球飞行的路线呈一条抛物线，如果网球距离地面的高度h（米）关于运行时间t（秒）的函数解析式为h=﹣ $\frac{1}{80}$ t²+ $\frac{1}{5}$ t+1（0≤t≤20），那么网球到达最高点时距离地面的高度是（）

A、1米 B、1.5米 C、1.6米 D、1.8米

查看试题解析
8. 飞机着陆后滑行的距离s（米）关于滑行的时间t（米）的函数解析式是s=60t﹣1.5t² ，则飞机着陆后滑行到停止下列，滑行的距离为（）

A、500米 B、600米 C、700米 D、800米

查看试题解析
9. 军事演习时发射一颗炮弹，经xs后炮弹的高度为ym，且时间x（s）与高度y（m）之间的函数关系为y=ax²+bx（a≠0），若炮弹在第8s与第14s时的高度相等，则在下列哪一个时间的高度是最高的（　　）

A、第9s B、第11s C、第13s D、第15s

查看试题解析
10. 如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x﹣k）²+h．已知球与O点的水平距离为6m时，达到最高2.6m，球网与O点的水平距离为9m．高度为2.43m，球场的边界距O点的水平距离为18m，则下列判断正确的是（）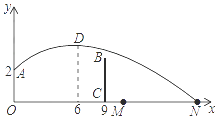

A、球不会过网 B、球会过球网但不会出界 C、球会过球网并会出界 D、无法确定

查看试题解析

二、填空题

11. 飞机着陆后滑行的距离s（单位：米）关于滑行的时间t（单位：秒）的函数解析式是s=60t﹣ $\frac{3}{2}$ t² ，则飞机着陆后滑行的最长时间为秒．

查看试题解析
12. 如图，在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角边上，C点在斜边上，设矩形的一边AB=xm，矩形的面积为ym² ，则y的最大值为．

查看试题解析
13. 已知：如图，用长为18m的篱笆（3AB+BC），围成矩形花圃．一面利用墙（墙足够长），则围成的矩形花圃ABCD的占地面积最大为m² ．

查看试题解析
14. 某菜农搭建了一个横截面为抛物线的大棚，尺寸如图，若菜农身高为1.8m，他在不弯腰的情况下，在棚内的横向活动范围是 m．

查看试题解析
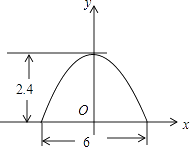15. 用一根长为16cm的铁丝围成一个矩形，则围成矩形面积的最大值是cm² ．

查看试题解析
16. 张力同学在校运动会上投掷标枪，标枪运行的高度h（m）与水平距离x（m）的关系式为h=﹣ $\frac{1}{48}$ x²+ $\frac{46}{48}$ x+2，则大力同学投掷标枪的成绩是m．

查看试题解析

三、解答题

17. 为了改善小区环境，某小区决定要在一块一边靠墙（墙长 25m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为 40m 的栅栏围住（如图）．设绿化带的BC 边长为x m，绿化带的面积为y m² ．

(1)、求y 与x 之间的函数关系式，并写出自变量x 的取值范围．

(2)、当x 为何值时，满足条件的绿化带的面积最大？

查看试题解析
18. 某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中的建筑材料可建围墙的总长为50m．设饲养室长为x（m），占地面积为y（m²）．

(1)、如图1，问饲养室长x为多少时，占地面积y最大？

(2)、如图2，现要求在图中所示位置留2m宽的门，且仍使饲养室的占地面积最大，小敏说：“只要饲养室长比（1）中的长多2m就行了．”请你通过计算，判断小敏的说法是否正确．

查看试题解析

t	0	1	2	3	4	5	6	7	…
h	0	8	14	18	20	20	18	14	…