2017-2018学年北师大版数学九年级下册同步训练:2.2.4 二次函数的图象与性质
试卷更新日期:2018-03-09 类型:同步测试
一、选择题
-
1. 已知函数y=ax2+bx+c的图象如图所示,则函数y=ax+b的图象是( )
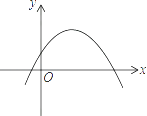 A、
A、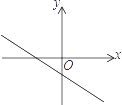 B、
B、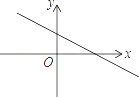 C、
C、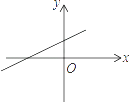 D、
D、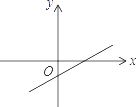 2. 一次函数y=ax+b(a≠0)与二次函数y=ax2+2x+b(a≠0)在同一直角坐标系中的图象可能是( )
2. 一次函数y=ax+b(a≠0)与二次函数y=ax2+2x+b(a≠0)在同一直角坐标系中的图象可能是( )
A、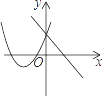 B、
B、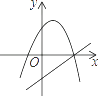 C、
C、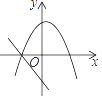 D、
D、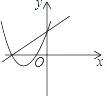 3. 抛物线y=x2﹣2x+m2+2(m是常数)的顶点在( )
3. 抛物线y=x2﹣2x+m2+2(m是常数)的顶点在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A、(1,﹣5) B、(3,﹣13) C、(2,﹣8) D、(4,﹣20)5. 二次函数y=x2﹣4x﹣4的顶点坐标为( )A、(2,﹣8) B、(2,8) C、(﹣2,8) D、(﹣2,﹣8)6. 二次函数y=mx2﹣nx﹣2过点(1,0),且函数图象的顶点在第三象限,当m+n为整数时,则mn的值为( )
A、﹣ ,﹣1 B、﹣ ,﹣2 C、﹣ , ,﹣2 D、 ,﹣27. 抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,且经过点(3,0),则a﹣b+c的值为( )A、﹣1 B、0 C、1 D、28. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac.
其中正确的结论的有( )
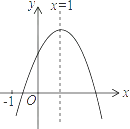 A、2个 B、3个 C、4个 D、5个9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列命题中正确的是( )
A、2个 B、3个 C、4个 D、5个9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列命题中正确的是( )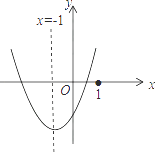 A、a>b>c B、一次函数y=ax+c的图象不经第四象限 C、m(am+b)+b<a(m是任意实数) D、3b+2c>010. 若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A、a>b>c B、一次函数y=ax+c的图象不经第四象限 C、m(am+b)+b<a(m是任意实数) D、3b+2c>010. 若抛物线y=x2﹣2x+m的最低点的纵坐标为n,则m﹣n的值是( )
A、﹣1 B、0 C、1 D、2二、填空题
-
11. 如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 .
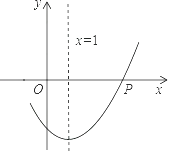 12. 如果抛物线y=﹣2x2+bx+3的对称轴是x=1,那么b= .13. 抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 .14. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 .
12. 如果抛物线y=﹣2x2+bx+3的对称轴是x=1,那么b= .13. 抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 .14. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 .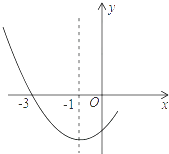 15. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号).
15. 抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号).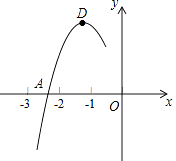 16. 如图为函数:y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是 .
16. 如图为函数:y=x2﹣1,y=x2+6x+8,y=x2﹣6x+8,y=x2﹣12x+35在同一平面直角坐标系中的图象,其中最有可能是y=x2﹣6x+8的图象的序号是 .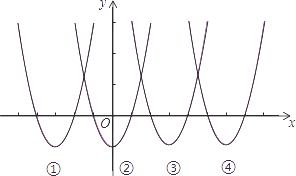
三、解答题