难点十二 推理与新定义问题
试卷更新日期:2018-03-08 类型:二轮复习
一、单选题
-
1. 欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占用非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式可知,e2i表示的复数在复平面中位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若数列{an}满足 =0,n∈N* , p为非零常数,则称数列{an}为“梦想数列”.已知正项数列 为“梦想数列”,且b1b2b3…b99=299 , 则b8+b92的最小值是( )A、2 B、4 C、6 D、83. 三角形的面积为a,b,c为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )A、 B、 C、 , (h为四面体的高) D、(S1 , S2 , S3 , S4分别为四面体的四个面的面积,r为四面体内切球的半径)4. 对于集合A,如果定义了一种运算“⊕”,使得集合A中的元素间满足下列4个条件:
(Ⅰ)∀a,b∈A,都有a⊕b∈A
(Ⅱ)∃e∈A,使得对∀a∈A,都有e⊕a=a⊕e=a;
(Ⅲ)∀a∈A,∃a′∈A,使得a⊕a′=a′⊕a=e;
(Ⅳ)∀a,b,c∈A,都有(a⊕b)⊕c=a⊕(b⊕c),
则称集合A对于运算“⊕”构成“对称集”.下面给出三个集合及相应的运算“⊕”:
①A={整数},运算“⊕”为普通加法;
②A={复数},运算“⊕”为普通减法;
③A={正实数},运算“⊕”为普通乘法.
其中可以构成“对称集”的有( )
A、①② B、①③ C、②③ D、①②③5. 记录k(k≤n)个点的颜色,称为该圆的一个“k阶段序”,当且仅当两个k阶色序对应位置上的颜色至少有一个不相同时,称为不同的k阶色序.若某圆的任意两个“k阶段序”均不相同,则称该圆为“k阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )A、4 B、6 C、8 D、106. 中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式(如图所示),表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如6613用算筹表示就是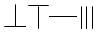 ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )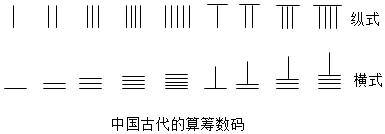 A、
A、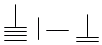 B、
B、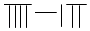 C、
C、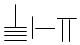 D、
D、 7. 若直角坐标平面内的两点P、Q满足条件:
7. 若直角坐标平面内的两点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;
②P、Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(点对[P,Q]与[Q,P]看作同一对“友好点对”),
已知函数f(x)= , 则此函数的“友好点对”有( )
A、0对 B、1对 C、2对 D、3对8. 定义区间[x1 , x2]长度为x2﹣x1 , (x2>x1),已知函数f(x)= (a∈R,a≠0)的定义域与值域都是[m,n],则区间[m,n]取最大长度时a的值为( )
A、 B、a>1或a<﹣3 C、a>1 D、39. 设函数f(x)的定义域为D,若f(x)满足条件:存在[a,b]⊆D,使f(x)在[a,b]上的值域是[ , ],则成f(x)为“倍缩函数”,若函数f(x)=log2(2x+t)为“倍缩函数”,则t的范围是( )A、(0, ) B、(0,1) C、(0, ] D、( ,+∞)10. 已知函数y=f(x)与y=F(x)的图象关于y轴对称,当函数y=f(x)和y=F(x)在区间[a,b]同时递增或同时递减时,把区间[a,b]叫做函数y=f(x)的“不动区间”.若区间[1,2]为函数f(x)=|2x﹣t|的“不动区间”,则实数t的取值范围是( )A、(0,2] B、[ ,+∞) C、[ ,2] D、[ ,2]∪[4,+∞)11. 设函数f(x),g(x)的定义域分别为F、G,且F⊆G.若对任意的x∈F,都有g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数”.已知函数f(x)=2x(x≤0),若g(x)为f(x)在R上一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是( )A、g(x)=2|x| B、g(x)=log2|x| C、 D、12. 符合以下性质的函数称为“S函数”:①定义域为R,②f(x)是奇函数,③f(x)<a(常数a>0),④f(x)在(0,+∞)上单调递增,⑤对任意一个小于a的正数d,至少存在一个自变量x0 , 使f(x0)>d.下列四个函数中 , , , 中“S函数”的个数为( )A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 设S为复数集C的非空子集.如果
(1)S含有一个不等于0的数;
(2)∀a,b∈S,a+b,a﹣b,ab∈S;
(3)∀a,b∈S,且b≠0,∈S,那么就称S是一个数域.
现有如下命题:
①如果S是一个数域,则0,1∈S;
②如果S是一个数域,那么S含有无限多个数;
③复数集是数域;
④S={a+b|a,b∈Q,}是数域;
⑤S={a+bi|a,b∈Z}是数域.
其中是真命题的有 (写出所有真命题的序号).
14. 设函数f(x)= (x>0),观察:f1(x)=f(x)= ,
f2(x)=f(f1(x))= ;
f3(x)=f(f2(x))= .
f4(x)=f(f3(x))=
…
根据以上事实,当n∈N*时,由归纳推理可得:fn(1)= .
15. 设函数f(x)的定义域为D,若存在非零实数m,使得对于任意x∈M(M⊆D),有(x﹣m)∈D且f(x﹣m)≤f(x),则称f(x)为M上的m度低调函数.如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x﹣a2|﹣a2 , 且f(x)为R上的5度低调函数,那么实数a的取值范围为 .16. 在直角坐标系 中,已知任意角 以坐标原点 为顶点,以 轴的非负半轴为始边,若其终边经过点 ,且 ,定义: ,称“ ”为“ 的正余弦函数”,若 ,则 .
17. 若数列{an}满足a2﹣a1>a3﹣a2>a4﹣a3>…>an+1﹣an>…,则称数列{an}为“差递减”数列,若数列{an}是“差递减”数列,且其通项an与其前n项和Sn(n∈N*)满足2Sn=3an+2λ﹣1(n∈N*),则实数λ的取值范围是三、解答题
-
18. 已知首项为 的等比数列{an}的前n项和为Sn , n∈N* , 且﹣2S2 , S3 , 4S4成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)对于数列 ,若存在一个区间M,均有Ai∈M,(i=1,2,3…),则称M为数列 的“容值区间”,设 ,试求数列{bn}的“容值区间”长度的最小值.
四、综合题
-
19. 记max{m,n}表示m,n中的最大值,如max .已知函数f(x)=max{x2﹣1,2lnx},g(x)=max{x+lnx,ax2+x}.(1)、求函数f(x)在 上的值域;(2)、试探讨是否存在实数a,使得g(x)< x+4a对x∈(1,+∞)恒成立?若存在,求a的取值范围;若不存在,说明理由.20. 若存在常数k(k∈N* , k≥2)、q、d,使得无穷数列{an}满足 则称数列{an}为“段比差数列”,其中常数k、q、d分别叫做段长、段比、段差.设数列{bn}为“段比差数列”.(1)、若{bn}的首项、段长、段比、段差分别为1、3、q、3.
①当q=0时,求b2016;
②当q=1时,设{bn}的前3n项和为S3n , 若不等式 对n∈N*恒成立,求实数λ的取值范围;
(2)、设{bn}为等比数列,且首项为b,试写出所有满足条件的{bn},并说明理由.
-