2017-2018学年北师大版数学八年级下册同步训练：2.2 不等式的基本性质

试卷更新日期：2018-03-08 类型：同步测试

进入出卷网下载

一、填空题

1. 不等式两边加(或减)同一个数(或式子),不等号的方向不变,即如果a>b,那么a±cb±c.

查看试题解析
2. 不等式两边乘(或除以)同一个正数，不等号的方向不变，即如果a>b，c>0，那么acbc $(或 \frac{a}{c}$ $\frac{b}{c})$ .

查看试题解析
3. 不等式两边乘(或除以)同一个数，不等号的方向改变，即如果a>b，c<0，那么ac < bc.(或 $\frac{a}{c}$ $\frac{b}{c}$ )

查看试题解析
4. 填空题

(1)、若ab,则b<a,即不等式具有对称性；

(2)、若a>b,b>c,则ac,即不等式具有同向传递性.

查看试题解析
5. 若2x>y,则y2x(填“>”或“<”).

查看试题解析

二、选择题

6. 已知实数a，b，若a>b，则下列结论正确的是（）

A、a-5<b-5 B、2+a<2+b C、 $\frac{a}{3} < \frac{b}{3}$ D、-3a>-3b

查看试题解析
7. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
8. 若m>n，则下列不等式不一定成立的是（）

A、m+2>n+2 B、2m>2n C、 $\frac{m}{2} > \frac{n}{2}$ D、m²>n²

查看试题解析
9. 给出下列结论：
①由2a>3，得a> $\frac{3}{2}$ ；②由2-a<0，得a>2；
③由a>b，得-3a>-3b；④由a>b，得a-9>b-9.
其中，正确的结论共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 下列不等式变形正确的是（）

A、由a>b得ac>bc B、由a>b得-2a>-2b C、由a>b得-a<-b D、由a>b得a-2<b-2

查看试题解析
11. 实数a，b，c在数轴上对应的点如图所示，则下列式子中正确的是（）

A、a-c>b-c B、a+c<b+c C、ac>bc D、 $\frac{a}{b} < \frac{c}{b}$

查看试题解析
12. 如图，a，b，c分别表示三种物体的质量，则下列判断正确的是（）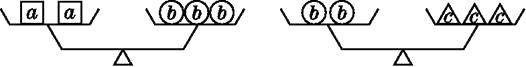

A、a<c B、a<b C、a>c D、b<c

查看试题解析
13. 当0<x<1时，x， $\frac{1}{x}$ ，x²的大小顺序是（）

A、 $\frac{1}{x}$ <x<x² B、x<x²< $\frac{1}{x}$ C、x²<x< $\frac{1}{x}$ D、 $\frac{1}{x}$ <x²<x

查看试题解析
14. 设“ ▲ ”“●”“■”分别表示三种不同的物体，现用天平称了两次，情况如图所示，那么 ▲、●、■这三种物体按质量从大到小排列应为（）

A、■、●、▲ B、▲、■、● C、■、▲、● D、●、▲、■

查看试题解析

三、综合题

15. 说明下列不等式是怎样变形的：

(1)、若3<x+2，则x>1；

(2)、若 $\frac{1}{2}$ x<-1，则x<-2；

(3)、若- $\frac{3}{2}$ x>-6，则x<4；

(4)、若-3x>2，则x<- $\frac{2}{3}$ ；

(5)、若2x+3>-7，则x>-5；

(6)、若-2x+3<x+1，则x> $\frac{2}{3}$ .

查看试题解析
16. 指出下列各式成立的条件:

(1)、由mx<n,得x< $\frac{n}{m}$ ;

(2)、由a<b,得ma>mb;

(3)、由a>-5,得a²≤-5a;

(4)、由3x>4y,得3x-m>4y-m.

查看试题解析
17. 已知关于x的不等式(1-a)x>2两边都除以1-a,得x< $\frac{2}{1 - a}$ ,试化简:|a-1|+|a+2|.

查看试题解析
18. 根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:

(1)、若A-B>0,则AB;

(2)、若A-B=0,则AB;

(3)、若A-B<0,则AB.

(4)、以上这种比较大小的方法称为“作差法”.请运用这种方法尝试解决下面的问题:比较4+3a²-2b+b²与3a²-2b+1的大小.

查看试题解析
19. 现有不等式的性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:

(1)、利用性质①比较2a与a的大小(a≠0);

(2)、利用性质②比较2a与a的大小(a≠0).

查看试题解析