2017-2018学年北师大版数学八年级下册同步训练：1.4 角平分线 课时2 三角形的角平分线
试卷更新日期：2018-03-08 类型：同步测试
一、填空题
-
1. 三角形的三条内角平分线相交于一点,并且这一点到相等.
2. 如图，点P为△ABC三条角平分线的交点，PD⊥AB，PE⊥BC，PF⊥AC，则PDPEPF.
3. 如图，小林已经画出了一个三角形的两条角平分线，他说：“我不用再将第三个角平分，就能画出第三条角平分线.”他说的有道理吗?他会怎样做?答：.他这样做的理由是什么?答：.
二、选择题
-
4. 如图，在△ABC中，∠ABC，∠ACB的平分线相交于O，下列结论正确的是（ ）
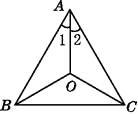A、∠1>∠2 B、∠1=∠2 C、∠1<∠2 D、不能确定∠1与∠2的大小关系5. 如图是尺规作图的痕迹，下列说法不正确的是（ ）
A、AE，BF是△ABC的内角平分线 B、CG也是△ABC的一条内角平分线 C、点O到△ABC三边的距离相等 D、AO=BO=CO6. 已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA=PB.下列确定P点的方法正确的是（ ）A、P为∠A与∠B的平分线的交点 B、P为∠A的平分线与AB的垂直平分线的交点 C、P为AC，AB两边上的高的交点 D、P为AC，AB两边的垂直平分线的交点7. 如图，△ABC的三边AB，BC，CA的长分别是20，30，40，其三条角平分线将△ABC分为三个三角形，则S△ABO∶S△BCO∶S△CAO等于（ ）
A、1∶1∶1 B、1∶2∶3 C、2∶3∶4 D、3∶4∶58. 如图，在△ABC中，∠ABC，∠ACB的平分线的交点P恰好在BC边的高AD上，则△ABC一定是（ ）
A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形三、解答题
