高中数学人教版必修5 第一章 解三角形 1.2 应用举例 同步练习
试卷更新日期:2018-03-08 类型:同步测试
一、选择题
-
1. 某人向正东方向走 后,向右转 ,然后朝新方向走 ,结果他离出发点恰好 ,那么 的值为 ( )A、 B、 C、 或 D、2. 海上有 两个小岛相距 ,从 岛望 岛和 岛,成 的视角,从 岛望 岛和 岛,成 的视角,则 间的距离为 ( )A、 B、 C、 D、3. 在△ABC中,A=60°,AB=2,且△ABC的面积S△ABC= ,则边BC的长为( )A、 B、2 C、 D、74. 如图,在塔底 的正西方 处测得塔顶的仰角为 ,在它的南偏东 的 处测得塔顶的仰角为 ,若 的距离是 ,则塔高为 ( )
 A、 B、 C、 D、5. 某校运动会开幕式上举行升旗仪式,在坡度为 的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为 和 ,第一排和最后一排的距离为 (如图所示),则旗杆的高度为( )
A、 B、 C、 D、5. 某校运动会开幕式上举行升旗仪式,在坡度为 的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为 和 ,第一排和最后一排的距离为 (如图所示),则旗杆的高度为( ) A、 B、 C、 D、6. 如图所示,长为 的木棒 斜靠在石堤旁,木棒的一端 在离堤足 处 的地面上,另一端 在离堤足 处 的石堤上,石堤的倾斜角为 ,则坡度值 等于 ( )
A、 B、 C、 D、6. 如图所示,长为 的木棒 斜靠在石堤旁,木棒的一端 在离堤足 处 的地面上,另一端 在离堤足 处 的石堤上,石堤的倾斜角为 ,则坡度值 等于 ( ) A、 B、 C、 D、7. 如图所示, , , 三点在地面上的同一直线上, ,从 两点测得 点的仰角分别为 , ,则 点离地面的高为 ( )
A、 B、 C、 D、7. 如图所示, , , 三点在地面上的同一直线上, ,从 两点测得 点的仰角分别为 , ,则 点离地面的高为 ( ) A、 B、 C、 D、8. 蓝军和红军进行军事演练,蓝军在距离 的军事基地 和 ,测得红军的两支精锐部队分别在 处和 处,且 , , , ,如图所示,则红军这两支精锐部队间的距离是 ( )
A、 B、 C、 D、8. 蓝军和红军进行军事演练,蓝军在距离 的军事基地 和 ,测得红军的两支精锐部队分别在 处和 处,且 , , , ,如图所示,则红军这两支精锐部队间的距离是 ( )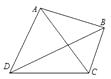 A、 B、 C、 D、9. 如图,为了测量某障碍物两侧A,B间的距离(此障碍物阻挡了A,B之间的视线),给定下列四组数据,测量时应当用数据
A、 B、 C、 D、9. 如图,为了测量某障碍物两侧A,B间的距离(此障碍物阻挡了A,B之间的视线),给定下列四组数据,测量时应当用数据 A、 B、 C、 D、10. 某观察站C与两灯塔A,B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30°,灯塔B在观察站C正西方向,则两灯塔A,B间的距离为A、500米 B、600米 C、700米 D、800米11. 如图,某工程中要将一长为100 m、倾斜角为75°的斜坡改造成倾斜角为30°的斜坡,并保持坡高不变,则坡底需加长
A、 B、 C、 D、10. 某观察站C与两灯塔A,B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30°,灯塔B在观察站C正西方向,则两灯塔A,B间的距离为A、500米 B、600米 C、700米 D、800米11. 如图,某工程中要将一长为100 m、倾斜角为75°的斜坡改造成倾斜角为30°的斜坡,并保持坡高不变,则坡底需加长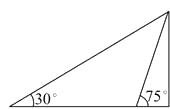 A、100 m B、100 m C、50( )m D、200 m12. 某人向正东方向走了x km后向右转了150°,然后沿新方向走了3 km,结果离出发点恰好为 km,那么x的值为A、 B、2 C、3 D、2 或13. 三角形的两边长分别为3和5,其夹角 的余弦值是方程 的根,则该三角形的面积为A、6 B、 C、8 D、1014. 如图,巡航艇在海上以 的速度沿南偏东 的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东 ,航行 到达C处,观测灯塔A的方向是北偏东 ,则巡航艇到达C处时,与灯塔A的距离是
A、100 m B、100 m C、50( )m D、200 m12. 某人向正东方向走了x km后向右转了150°,然后沿新方向走了3 km,结果离出发点恰好为 km,那么x的值为A、 B、2 C、3 D、2 或13. 三角形的两边长分别为3和5,其夹角 的余弦值是方程 的根,则该三角形的面积为A、6 B、 C、8 D、1014. 如图,巡航艇在海上以 的速度沿南偏东 的方向航行.为了确定巡航艇的位置,巡航艇在B处观测灯塔A,其方向是南偏东 ,航行 到达C处,观测灯塔A的方向是北偏东 ,则巡航艇到达C处时,与灯塔A的距离是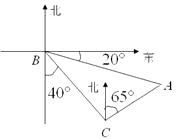 A、 B、 C、 D、15. 在 中,已知A=30°,a=8,b=8 ,则 的面积为A、 B、16 C、 或16 D、 或16. 一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以每小时32海里的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8 海里,则灯塔S在B处的( )
A、 B、 C、 D、15. 在 中,已知A=30°,a=8,b=8 ,则 的面积为A、 B、16 C、 或16 D、 或16. 一艘客船上午9:30在A处,测得灯塔S在它的北偏东30°,之后它以每小时32海里的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8 海里,则灯塔S在B处的( )
A、北偏东75° B、北偏东75°或东偏南75° C、东偏南75° D、以上方位都不对二、填空题
-
17. 三角形一边长为 ,它对的角为 ,另两边之比为 ,则此三角形面积为 .
18. 在相距 千米的 , 两点处测量目标点 ,若 , ,则 , 两点之间的距离为千米.19. 某舰艇在 处测得遇险渔船在北偏东 方向上的 处,且到 的距离为 海里,此时得知,该渔船沿南偏东 方向,以每小时 海里的速度向一小岛靠近,舰艇的速度为 海里/小时,则舰艇到达渔船的最短时间是小时.20. 如图,线段AB,CD分别表示甲、乙两楼,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C处的仰角为 =30°,测得乙楼底部D的俯角 =60°,已知甲楼的高AB=24米,则乙楼的高 米. 21. 甲船在岛B的正南A处,AB=10 km,甲船以每小时4 km的速度向正北航行,同时,乙船自B出发以每小时6 km的速度向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间是h.22. 如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,则此舰触礁的危险.(填“有”或“没有”)
21. 甲船在岛B的正南A处,AB=10 km,甲船以每小时4 km的速度向正北航行,同时,乙船自B出发以每小时6 km的速度向北偏东60°的方向驶去.当甲、乙两船相距最近时,它们所航行的时间是h.22. 如图,海中有一小岛B,周围3.8海里内有暗礁.一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北偏东60°.若此舰不改变航行的方向继续前进,则此舰触礁的危险.(填“有”或“没有”) 23. 如图,一辆汽车在一条水平的公路上向正西行驶,到 处时测得公路北侧一山顶D在西偏北 的方向上,行驶600 m后到达 处,测得此山顶在西偏北 的方向上,仰角为 ,则此山的高度 m.
23. 如图,一辆汽车在一条水平的公路上向正西行驶,到 处时测得公路北侧一山顶D在西偏北 的方向上,行驶600 m后到达 处,测得此山顶在西偏北 的方向上,仰角为 ,则此山的高度 m.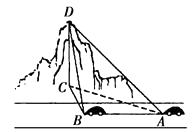
三、解答题
-
24. 如图,地面上有一旗杆 ,为了测量它的高度,在地面上选一条基线 ,测得 ,在 处测得点 的仰角为 ,在 处测得点 的仰角为 ,同时可测得 ,求旗杆的高度.
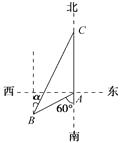
 25. 某人在塔 的正东 处沿着南偏西 的方向前进 米后到达 处,望见塔在东北方向,若沿途测得塔的最大仰角为 ,求塔高.26. 某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶.公路的走向是M站的北偏东40°.开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站?
25. 某人在塔 的正东 处沿着南偏西 的方向前进 米后到达 处,望见塔在东北方向,若沿途测得塔的最大仰角为 ,求塔高.26. 某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶.公路的走向是M站的北偏东40°.开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站?