备考2018年中考数学一轮基础复习：专题三 因式分解

试卷更新日期：2018-03-07 类型：一轮复习

进入 出卷网 下载

一、单选题

  • 1. 下列各式中，能用平方差公式分解因式的是（    ）

    A、x2+y2 B、x2-y2 C、–x2-y2 D、x-y2

    查看试题解析

  • 2. 把多项式x2+ax+b分解因式，得（x+1）（x﹣3）则a，b的值分别是（　　）

    A、a=2，b=3 B、a=﹣2，b=﹣3 C、a=﹣2，b=3 D、a=2，b=﹣3

    查看试题解析

  • 3. 如图，边长为a，b的矩形的周长为14，面积为10，则a2b+ab2的值为（   ）

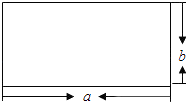    A、140 B、70 C、35 D、24

    查看试题解析

  • 4. 若a，b为两质数且相差2，则ab+1之值可能为下列何者（   ）
    A、392 B、402 C、412 D、422

    查看试题解析

  • 5. 下列多项式中，能用完全平方式分解的是（   ）

    A、x2﹣x+1 B、1﹣2xy+x2y2 C、a2+a+12 D、﹣a2+b2﹣2ab

    查看试题解析

  • 6. a、b、c为某一三角形的三边，且满足a2+b2+c2=6a+8b+10c﹣50，则三角形是（   ）
    A、直角三角形 B、等边三角形 C、等腰三角形 D、锐角三角形

    查看试题解析

  • 7. 将下列多项式分解因式，结果中不含因式x﹣1的是（   ）

    A、x2﹣1 B、x2+2x+1 C、x2﹣2x+1 D、x（x﹣2）﹣（x﹣2）

    查看试题解析

  • 8. 多项式mx2﹣m与多项式x2﹣2x+1的公因式是（　　）


    A、x﹣1 B、x+1 C、x2﹣1 D、（x﹣1）2

    查看试题解析

  • 9. 下列各式由左到右的变形中，属于分解因式的是（   ）
    A、a（m+n）=am+an B、a2﹣b2﹣c2=（a﹣b）（a+b）﹣c2 C、10x2﹣5x=5x（2x﹣1） D、x2﹣16+6x=（x+4）（x﹣4）+6x

    查看试题解析

  • 10. 已知：a=2014x+2015，b=2014x+2016，c=2014x+2017，则a2+b2+c2﹣ab﹣ac﹣bc的值是（   ）
    A、0 B、1 C、2 D、3

    查看试题解析

  • 11. 两个连续的奇数的平方差总可以被k整除，则k的最大值等于（   ）

    A、4 B、8 C、4或﹣4 D、8的倍数

    查看试题解析

  • 12. 多项式77x2﹣13x﹣30可因式分解成（7x+a）（bx+c），其中a、b、c均为整数，求a+b+c之值为何？（　　）

    A、8 B、10 C、12 D、22

    查看试题解析

  • 13. 已知甲、乙、丙均为x的一次多项式，且其一次项的系数皆为正整数．若甲与乙相乘为x2﹣4，乙与丙相乘为x2+15x﹣34，则甲与丙相加的结果与下列哪一个式子相同？（　　）

    A、2x+19 B、2x﹣19 C、2x+15 D、2x﹣15

    查看试题解析

  • 14. 把8a3﹣8a2+2a进行因式分解，结果正确的是（　　）

    A、2a（4a2﹣4a+1） B、8a2（a﹣1） C、2a（2a﹣1）2 D、2a（2a+1）2

    查看试题解析

  • 15. n是整数，式子 18  [1﹣（﹣1）n]（n2﹣1）计算的结果（　　）

    A、是0 B、总是奇数 C、总是偶数 D、可能是奇数也可能是偶数

    查看试题解析

二、填空题

  • 16. 在实数范围内因式分解：x5﹣4x= ．

    查看试题解析

  • 17. 分解因式：3x2﹣18x+27= ．

    查看试题解析

  • 18. 已知x+y= 3 ，xy= 6 ，则x2y+xy2的值为 ．

    查看试题解析

  • 19. 若实数x满足x2﹣2x﹣1=0，则2x3﹣7x2+4x﹣2017= ．

    查看试题解析

  • 20.

    阅读理解：用“十字相乘法”分解因式2x2﹣x﹣3的方法．

    （i）二次项系数2=1×2；

    （ii）常数项﹣3=﹣1×3=1×（﹣3），验算：“交叉相乘之和”；

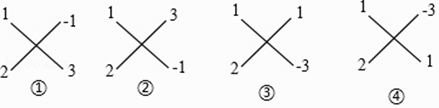
    1×3+2×（﹣1）=1     1×（﹣1）+2×3=5     1×（﹣3）+2×1=﹣1     1×1+2×（﹣3）=﹣5

    （iii）发现第③个“交叉相乘之和”的结果1×（﹣3）+2×1=﹣1，等于一次项系数﹣1．

    即：（x+1）（2x﹣3）=2x2﹣3x+2x﹣3=2x2﹣x﹣3，则2x2﹣x﹣3=（x+1）（2x﹣3）．

    像这样，通过十字交叉线帮助，把二次三项式分解因式的方法，叫做十字相乘法．仿照以上方法，分解因式：3x2+5x﹣12= ．

    查看试题解析

三、计算题

  • 21. 化简求值：（1﹣ 122 ）（1﹣ 132 ）（1﹣ 142 ）（1﹣ 152 ）（1﹣ 162 ）（1﹣ 172 ）（1﹣ 182 ）

    查看试题解析

  • 22. 利用因式分解计算：
    (1)、342+34×32+162；
    (2)、38.92﹣2×38.9×48.9+48.92 ．

    查看试题解析

四、综合题

  • 23. 在日常生活中我们经常用到密码，如取款、上网购物需要密码，有一种用因式分解法产生密码，方便记忆，其原理是：将一个多项式因式分解：例如x4﹣y4=（x2+y2）（x+y）（x﹣y），当x=8，y=9时，x2+y2=145，x+y=17，x﹣y=4则可以得到密码是145174，1741454…，等等，根据上述方法

    当x=32，y=12时，对于多项式x2y﹣y3分解因式后可以形成哪些数字密码？

    查看试题解析

  • 24. 对任意一个三位数n，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为F（n）．例如n=123，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为213+321+132=666，666÷111=6，所以F（123）=6．
    (1)、计算：F（243），F（617）；
    (2)、若s，t都是“相异数”，其中s=100x+32，t=150+y（1≤x≤9，1≤y≤9，x，y都是正整数），规定：k= F(s)F(t) ，当F（s）+F（t）=18时，求k的最大值．

    查看试题解析

  • 25. 我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）= pq ．

    例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）= 34 ．

    （Ⅰ）如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．

    求证：对任意一个完全平方数m，总有F（m）=1；

    （Ⅱ）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”，求所有“吉祥数”；

    （Ⅲ）在（2）所得“吉祥数”中，求F（t）的最大值．

    查看试题解析