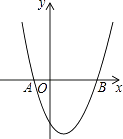新疆乌鲁木齐市2018届九年级上学期数学期末考试试卷

试卷更新日期：2018-03-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列标志既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将二次函数 $y = x^{2} - 2 x + 3$ 化为 $y = {(x - h)}^{2} + k$ 的形式，结果为（）

A、 $y = {(x - 1)}^{2} + 4$ B、 $y = {(x - 1)}^{2} + 2$ C、 $y = {(x + 1)}^{2} + 4$ D、 $y = {(x + 1)}^{2} + 2$

查看试题解析
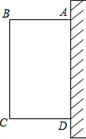
3. 下列事件中，必然事件是（）

A、抛掷 $1$ 枚质地均匀的骰子，向上的点数为 $6$ B、两直线被第三条直线所截，同位角相等 C、抛一枚硬币，落地后正面朝上 D、实数的绝对值是非负数

查看试题解析
4. 如图，点 $B$ 在⊙ $O$ 上，弦 $A C$ ∥ $O B$ ， $∠ B O C = 50 °$ ，则 $∠ O A B =$ （）

A、 $25 °$ B、 $50 °$ C、 $60 °$ D、 $30 °$

查看试题解析
5. 关于 $x$ 的一元二次方程 $(m - 2) x^{2} + 2 x + 1 = 0$ 有实数根，则 $m$ 的取值范围是（）

A、 $m \leq 3$ B、 $m < 3$ C、 $m < 3 且 m \neq 2$ D、 $m \leq 3 且 m \neq 2$

查看试题解析
6. 如图，在半径为 $5 c m$ 的⊙ $O$ 中，弦 $A B = 6 c m$ ， $O C ⊥ A B$ 于点 $C$ ，则 $O C =$ （）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
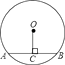7. 将一枚质地均匀的骰子掷两次，则两次点数之和等于 $9$ 的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{1}{9}$ D、 $\frac{1}{12}$

查看试题解析
8. 抛物线 $y = a x^{2} + b x + c$ 的部分图象如图所示（对称轴是 $x = 1$ ），若 $y < 0$ ，则 $x$ 的取值范围是（）

A、 $- 1 < x < 4$ B、 $- 1 < x < 3$ C、 $x < - 1$ 或 $x > 4$ D、 $x < - 1$ 或 $x > 3$

查看试题解析
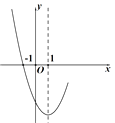9. 某商场将进价为 $20$ 元∕件的玩具以 $30$ 元∕件的价格出售时，每天可售出 $300$ 件，经调查当单价每涨 $1$ 元时，每天少售出 $10$ 件．若商场想每天获得 $3750$ 元利润，则每件玩具应涨多少元？若设每件玩具涨 $x$ 元，则下列说法错误的是（）

A、涨价后每件玩具的售价是 $(30 + x)$ 元 B、涨价后每天少售出玩具的数量是 $10 x$ 件 C、涨价后每天销售玩具的数量是 $(300 - 10 x)$ 件 D、可列方程为 $(30 + x) (300 - 10 x) = 3750$

查看试题解析
10. 如图，已知函数y＝ax²＋bx＋c $(a \neq 0)$ 的图象如图所示，有以下四个结论：①abc=0，② $a + b + c > 0$ ，③ $a > b$ ，④ $4 a c - b^{2} < 0$ ；其中正确的结论有（）

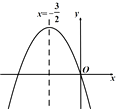A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若点 $M (3, a - 2)$ 与 $N (- 3, a)$ 关于原点对称，则 $a =$ ．

查看试题解析
12. 关于 $x$ 的 $x^{2} - a x - 3 a = 0$ 的一个根是 $x = - 2$ ，则它的另一个根是．

查看试题解析
13. 已知圆锥的底面半径是 $3 c m$ ，高为 $4 c m$ ，则其侧面积为 $c m^{2}$ ．

查看试题解析
14. 一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，小文在袋中放入10个白球（每个球除颜色外其余都与红球相同）．摇匀后每次随机从袋中摸出一个球，记下颜色后放回袋中，通过大量重复摸球试验后发现，摸到白球的频率是 $\frac{2}{7}$ ，则袋中红球约为个．

查看试题解析
15. 有一人患了流感，经过两轮传染后共有 $169$ 人患了流感，每轮传染中平均一个人传染了人．

查看试题解析
16. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90^{\circ}$ ， $A C = 5 c m ， B C = 12 c m$ ，将 $Δ A B C$ 绕点 $B$ 顺时针旋转 $60^{\circ}$ ，得到 $Δ E B D$ ，连接 $D C$ ，交 $A B$ 于点 $F$ ，则 $Δ A C F$ 与 $Δ B D F$ 的周长之和为 $c m$ .

查看试题解析

三、解答题

17. 解方程 $3 x (x - 2) = 2 (2 - x)$

查看试题解析
18. 某地区2015年投入教育经费2500万元，2017年投入教育经费3025万元.

(1)、求2015年至2017年该地区投入教育经费的年平均增长率；

(2)、根据(1)所得的年平均增长率，预计2018年该地区将投入教育经费多少万元.

查看试题解析
19. 如图，在 $R t △ A B C$ 中， $∠ B = 90^{\circ}$ ，AB=BC，A，B的坐标分别为 $(0 ， 4) ， (- 2 ， 4)$ ，将 $△ A B C$ 绕点P旋转 $180^{\circ}$ 后得到 $Δ A^{'} B^{'} C^{'}$ ，其中点B的对应点 $B^{'}$ 的坐标为 $(2 ， 2)$ ．

(1)、求出点C的坐标；

(2)、求点P的坐标，并求出点C的对应点 $C^{'}$ 的坐标．

查看试题解析
20. 有 $4$ 张看上去无差别的卡片，上面分别写着 $1 ， 2 ， 3 ， 4$ ，随机抽取 $1$ 张后，放回并混在一起，再随机抽取 $1$ 张．

(1)、请用树状图或列表法等方法列出各种可能出现的结果；

(2)、求两次抽到的卡片上的数字之和等于 $5$ 的概率．

查看试题解析
21. 如图，点 $D$ 在⊙ $O$ 的直径 $A B$ 的延长线上，点 $C$ 在⊙ $O$ 上， $A C = C D$ ， $∠ A C D = 120 °$ ．

(1)、求证： $C D$ 是⊙ $O$ 的切线；

(2)、若⊙ $O$ 的半径为 $2$ ，求图中阴影部分的面积．

查看试题解析
22. 如图所示，某小区要用篱笆围成一矩形花坛，花坛的一边用足够长的墙，另外三边所用的篱笆之和恰好为 $16$ 米．

(1)、求矩形 $A B C D$ 的面积（用 $s$ 表示，单位：平方米）与边 $A B$ （用 $x$ 表示，单位：米）之间的函数关系式（不要求写出自变量 $x$ 的取值范围）；怎样围，可使花坛面积最大？

(2)、如何围，可使此矩形花坛面积是 $30$ 平方米？

查看试题解析
23. 已知抛物线 $y = x^{2} + b x + c$ 经过 $A (- 1 ， 0) ， B (3 ， 0)$ 两点．

(1)、求抛物线的解析式和顶点坐标；

(2)、设点 $P$ 为抛物线上一点，若 $S_{Δ P A B} = 6$ ，求点 $P$ 的坐标．

查看试题解析