上海市金山区2018届九年级上学期数学期末考试试卷
试卷更新日期:2018-03-07 类型:期末考试
一、单选题
-
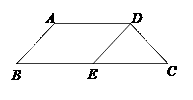
1. 已知:a、b是不等于0的实数,2a=3b,那么下列等式中正确的是( )A、 ; B、 ; C、 ; D、 .2. 在Rt△ABC中, , , , ,下列各式中正确的是( )A、 ; B、 ; C、 ; D、 .3. 将抛物线 平移,使平移后所得抛物线经过原点,那么平移的过程为( )A、向下平移3个单位; B、向上平移3个单位; C、向左平移4个单位; D、向右平移4个单位.4. 如图,梯形ABCD中,AD∥BC,AB=DC,DE∥AB,下列各式正确的是( )
 A、 ; B、 ; C、 ; D、 .5. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是( )
A、 ; B、 ; C、 ; D、 .5. 一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米,木工要以一根长为60厘米的木条为一边,做一个与模型三角形相似的三角形,那么另两条边的木条长度不符合条件的是( )
A、30厘米、45厘米; B、40厘米、80厘米; C、80厘米、120厘米; D、90厘米、120厘米6. 在Rt△ABC中,∠ACB=90°,AC=12,BC=9,D是AB的中点,G是△ABC的重心,如果以点D为圆心DG为半径的圆和以点C为圆心半径为 的圆相交,那么 的取值范围是( )
A、 ; B、 ; C、 ; D、 .二、填空题
-
7. 计算: .8. 计算: .9. 如果两个相似三角形对应边上的高的比为1∶4,那么这两个三角形的周长比是 .10. 在Rt△ABC中,∠C=90°,sinA= ,那么cosA= .11. 已知一个斜坡的坡度 ,那么该斜坡的坡角为 .12. 如图,E是▱ABCD的边AD上一点,AE= ED,CE与BD相交于点F,BD=10,那么DF= .
 13. 抛物线 的顶点坐标是 .14. 点(-1,a)、(-2,b)是抛物线 上的两个点,那么a和b的大小关系是a b(填“>”或“<”或“=”).15. 如图,AB是⊙O的弦,∠OAB=30°.OC⊥OA,交AB于点C,若OC=6,则AB的长等于 .
13. 抛物线 的顶点坐标是 .14. 点(-1,a)、(-2,b)是抛物线 上的两个点,那么a和b的大小关系是a b(填“>”或“<”或“=”).15. 如图,AB是⊙O的弦,∠OAB=30°.OC⊥OA,交AB于点C,若OC=6,则AB的长等于 . 16. 如果一个正多边形每一个内角都等于144°,那么这个正多边形的边数是 .17. 两圆内切,其中一个圆的半径长为6,圆心距等于2,那么另一个圆的半径长等于 .18. 如图,在矩形ABCD中,E是AD上一点,把△ABE沿直线BE翻折,点A正好落在BC边上的点F处,如果四边形CDEF和矩形ABCD相似,那么四边形CDEF和矩形ABCD面积比是 .
16. 如果一个正多边形每一个内角都等于144°,那么这个正多边形的边数是 .17. 两圆内切,其中一个圆的半径长为6,圆心距等于2,那么另一个圆的半径长等于 .18. 如图,在矩形ABCD中,E是AD上一点,把△ABE沿直线BE翻折,点A正好落在BC边上的点F处,如果四边形CDEF和矩形ABCD相似,那么四边形CDEF和矩形ABCD面积比是 .
三、解答题
-
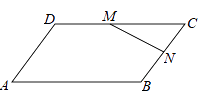
19. 计算: .20. 如图,已知平行四边形ABCD,点M、N分别是边DC、BC的中点,设 , ,求向量 关于 、 的分解式.
 21. 如图,已知AB是⊙O的弦,C是的中点,AB=8,AC= ,求⊙O半径的长.
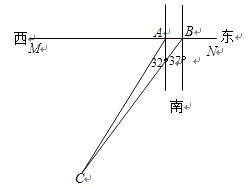
21. 如图,已知AB是⊙O的弦,C是的中点,AB=8,AC= ,求⊙O半径的长. 22. 如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.
22. 如图,MN是一条东西方向的海岸线,在海岸线上的A处测得一海岛在南偏西32°的方向上,向东走过780米后到达B处,测得海岛在南偏西37°的方向,求小岛到海岸线的距离.(参考数据:tan37°= cot53°≈0.755,cot37°= tan53°≈1.327,tan32°= cot58°≈0.625,cot32°= tan58°≈1.600.)
 23. 如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
23. 如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.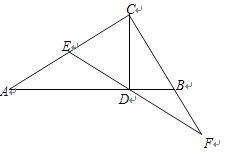 (1)、求证:DF是BF和CF的比例中项;(2)、在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.
(1)、求证:DF是BF和CF的比例中项;(2)、在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.
24. 平面直角坐标系xOy中(如图),已知抛物线y=ax2+bx+3与y轴相交于点C,与x轴正半轴相交于点A,OA=OC,与x轴的另一个交点为B,对称轴是直线x=1,顶点为P. (1)、求这条抛物线的表达式和顶点P的坐标;(2)、抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;(3)、点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.25. 如图,已知在△ABC中,AB=AC=5,cosB= ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)、求这条抛物线的表达式和顶点P的坐标;(2)、抛物线的对称轴与x轴相交于点M,求∠PMC的正切值;(3)、点Q在y轴上,且△BCQ与△CMP相似,求点Q的坐标.25. 如图,已知在△ABC中,AB=AC=5,cosB= ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD. (1)、求△ABC的面积;(2)、设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)、如果△APD是直角三角形,求PB的长.
(1)、求△ABC的面积;(2)、设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;(3)、如果△APD是直角三角形,求PB的长.