海南省定安县2018届九年级上学期数学期末考试试卷
试卷更新日期:2018-03-07 类型:期末考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则x的取值范围是( )A、x≥-3 B、x>3 C、x≥3 D、x≤32. 下列计算错误的是( )A、 B、 C、 D、3. 顺次连结矩形各边中点所得的四边形是( ).A、矩形 B、菱形 C、正方形 D、等腰梯形4. 若关于 的方程 (k为常数)有两个相等的实数根,则 的值为( )
A、﹣4 B、4 C、﹣ D、5. 如图所示,若△ABC∽△DEF,则∠E的度数为( )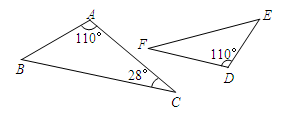 A、28° B、32° C、42° D、52°6. 如图,将△ABC沿DE翻折,折痕DE∥BC,若 ,BC=9 ,则DE的长等于( )
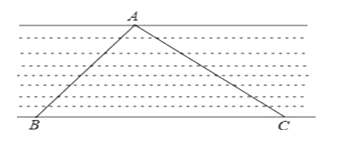
A、28° B、32° C、42° D、52°6. 如图,将△ABC沿DE翻折,折痕DE∥BC,若 ,BC=9 ,则DE的长等于( ) A、2 B、3 C、4 D、4.57. 如图,修建抽水站时,沿着坡度为i=1: 的斜坡铺设水管.若测得水管A处铅垂高度为8 m,则所铺设水管AC的长度为( )
A、2 B、3 C、4 D、4.57. 如图,修建抽水站时,沿着坡度为i=1: 的斜坡铺设水管.若测得水管A处铅垂高度为8 m,则所铺设水管AC的长度为( )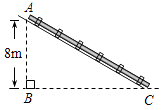 A、8m B、12m C、14m D、16m8. 将一元二次方程x2-4x-6=0化成(x-a)2=b的形式,则b等于( )A、4 B、6 C、8 D、109. 如图,铁路路基横断面为一个等腰梯形,若腰的坡度为i=3:2,顶宽是7米,路基高是6米,则路基的下底宽是( )
A、8m B、12m C、14m D、16m8. 将一元二次方程x2-4x-6=0化成(x-a)2=b的形式,则b等于( )A、4 B、6 C、8 D、109. 如图,铁路路基横断面为一个等腰梯形,若腰的坡度为i=3:2,顶宽是7米,路基高是6米,则路基的下底宽是( )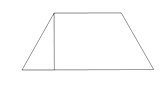 A、7米 B、11米 C、15米 D、17米10. 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端25米的B处,测得树顶A的仰角∠ABO为 ,则树OA的高度为 ( )
A、7米 B、11米 C、15米 D、17米10. 如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端25米的B处,测得树顶A的仰角∠ABO为 ,则树OA的高度为 ( ) A、 米 B、25 米 C、25 米 D、25 米11. 参加一次足球联赛的每两队之间都进行一场比赛,共有比赛55场,总共有( )支球队参加比赛.A、9 B、10 C、11 D、1212. 某班为迎接“体育健康周”活动,从3 名学生(1男 2女)中随机选两名担任入场式旗手,则选中两名女学生的概率是( )A、 B、 C、 D、13. 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=6,则DE的长为( )
A、 米 B、25 米 C、25 米 D、25 米11. 参加一次足球联赛的每两队之间都进行一场比赛,共有比赛55场,总共有( )支球队参加比赛.A、9 B、10 C、11 D、1212. 某班为迎接“体育健康周”活动,从3 名学生(1男 2女)中随机选两名担任入场式旗手,则选中两名女学生的概率是( )A、 B、 C、 D、13. 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E.若BC=6,则DE的长为( )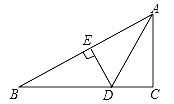 A、1 B、2 C、3 D、414. 如图,在平面直角坐标系中,△ABC位于第二象限,点C的坐标是(﹣1,1),先把△ABC向右平移5个单位长度得到△A1B1C1 , 再作与△A1B1C1关于 轴对称的△A2B2C2 , 则点C的对应点C2的坐标是( )
A、1 B、2 C、3 D、414. 如图,在平面直角坐标系中,△ABC位于第二象限,点C的坐标是(﹣1,1),先把△ABC向右平移5个单位长度得到△A1B1C1 , 再作与△A1B1C1关于 轴对称的△A2B2C2 , 则点C的对应点C2的坐标是( ) A、(4,1) B、(4,-1) C、(﹣6,1) D、(-6,-1)
A、(4,1) B、(4,-1) C、(﹣6,1) D、(-6,-1)二、填空题
-
15. 计算: = .16. 在△ABC中,∠C=90°,AB=10,BC=8,则cos A= .17. 如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,AD⊥BC于点D,则△ACD与△ABC的面积比为
 18. 如图,在边长为6的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则OF的长为 .
18. 如图,在边长为6的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则OF的长为 .
三、解答题
-
19. 计算:
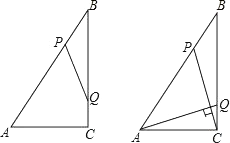
(1)、(2)、(3)、(1-cos60°)2+ .20. 如图,在Rt△ABC中,∠ABC=90°,BD⊥AC于点D ,点E为线段BC的中点,AD=2,tan A=2. (1)、求AB的长;(2)、求DE的长.21. 九年级某班从A、B、C、D四位同学中选出两名同学去参加学校的羽毛球双打比赛.(1)、请用树状图法,求恰好选中A、C两位同学的概率;(2)、若已确定B被选中,再从其余三位同学中随机选取一位,求恰好选中C同学的概率.22. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,3),B(-2,1),C(-3,1).
(1)、求AB的长;(2)、求DE的长.21. 九年级某班从A、B、C、D四位同学中选出两名同学去参加学校的羽毛球双打比赛.(1)、请用树状图法,求恰好选中A、C两位同学的概率;(2)、若已确定B被选中,再从其余三位同学中随机选取一位,求恰好选中C同学的概率.22. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,3),B(-2,1),C(-3,1). (1)、①画出△ABC关于y轴对称的△A1B1C1 , 并写出A1点的坐标及sin∠B1C1A1的值;
(1)、①画出△ABC关于y轴对称的△A1B1C1 , 并写出A1点的坐标及sin∠B1C1A1的值;②以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将△ABC放大后的△A2B2C2 , 并写出A2点的坐标;
(2)、若点D为线段BC的中点,直接写出经过(2)的变化后点D的对应点D2的坐标.