北京市燕山区2018届九年级上学期数学期末考试试卷
试卷更新日期：2018-03-06 类型：期末考试
一、单选题
-
1. 以下是回收、绿色包装、节水、低碳四个标志，其中为中心对称图形的是（ ）A、
B、
C、
D、
2. 将一枚硬币抛掷两次，则这枚硬币两次反面都向上的概率为（ ）
A、 B、 C、 D、3. 如图，圆心角∠AOB=25°，将弧AB旋转n°得到弧CD，则∠COD等于（ ）
A、25° B、25°+n° C、50° D、50°+n°4. 若点（x1 ， y1），（x2 ， y2）都是反比例函数 图象上的点，并且 ，则下列结论中正确的是（ ）
A、x1＞x2 B、x1＜x2 C、y随x的增大而减小 D、两点有可能在同一象限5. 已知：在Rt△ABC中，∠C=90°，sinA= ，则cosB的值为（ ）
A、 B、 C、 D、6. 如图，已知点P为反比例函数 上一点，过点P向坐标轴引垂线，垂足分别为M，N，那么四边形MONP的面积为（ ）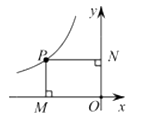
A、－6 B、3 C、6 D、127. 如图，⊙O的直径AB=4，BC切⊙O于点B，OC平行于弦AD，OC=5，则AD的长为（ ）
A、 B、 C、 D、8. 如图，△ABC．的三个顶点分别为A（1，2），B（5，2），C（5，5）．若反比例函数 在第一象限内的图象与△ABC有交点，则k的取值范围是（ ）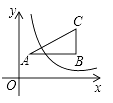
A、2≤k≤25 B、2≤k≤10 C、1≤k≤5 D、10≤k≤25二、填空题
-
9. 已知a是锐角， ，则a= ．
10. 点A（-2，5）在反比例函数 （k≠0）的图象上，则k的值是 ．
11. 如图，AB、AC是⊙O的弦，OM⊥AB，ON⊥AC，垂足分别为M、N．如果MN=2.5，那么BC= ．
12. 如图，一圆内切于四边形ABCD，且AB=16，CD=10，则四边形ABCD的周长为 ．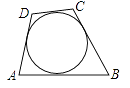
13. 如图，量角器的直径与直角三角尺ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3°的速度旋转，CP与量角器的半圆弧交于点E，则第20秒点E在量角器上对应的读数是°．
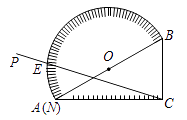14. 规定：sin（－x）＝－sinx，cos（－x）＝cosx，sin（x+y）＝sinx·cosy＋cosx·siny．据此判断下列等式成立的是（填序号）．①cos（－60°）＝—cos60°=
②sin75°＝sin（30°+45°）=sin30°·cos45°+cos30°·sin45°=
③sin2x＝sin（x+x）＝sinx·cosx+cosx·sinx＝2sinx·cosx；
④sin（x－y）＝sinx·cosy－cosx·siny．
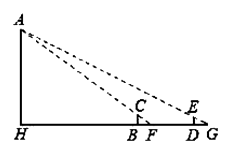
15. 我国魏晋时期数学家刘徽编撰的最早一部测量数学著作《海岛算经》中有一题：今有望海岛，立两表齐高三丈，前后相去千步，令后表与前表参相直．从前表却行一百二十三步，人目着地，取望岛峰，与表末参合．从后表却行一百二十七步，人目着地，取望岛峰，亦与表末参合．问岛高几何？
译文：今要测量海岛上一座山峰AH的高度，在B处和D处树立标杆BC和DE，标杆的高都是3丈，B和D两处相隔1000步（1丈=10尺，1步=6尺），并且AH，CB和DE在同一平面内．从标杆BC后退123步的F处可以看到顶峰A和标杆顶端C在同一直线上；从标杆ED后退127步的G处可以看到顶峰A和标杆顶端E在同一直线上．则山峰AH的高度是 ．
16. 在数学课上，老师提出利用尺规作图完成下面问题：已知：∠ACB是△ABC的一个内角
求作：∠APB=∠ACB
小路的作法如下：
已知：∠ACB是△ABC的一个内角．
求作：∠APB=∠ACB．
小路的作法如下：
如图，
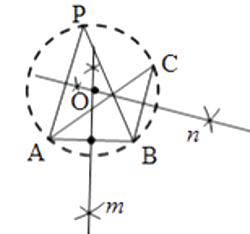
①作线段AB的垂直平分线m；
②作线段BC的垂直平分线n，与直线m交于点O；
③以点O为圆心，OA为半径作△ABC的外接圆；
④在优弧AC上取一点P，连结AP，BP.
所以∠APB=∠ACB.
老师说：“小路的作法正确．”
请回答：
(1)、点O为△ABC外接圆圆心（即OA=OB=OC）的依据是；
(2)、∠APB=∠ACB的依据是 ．
三、解答题
-
17. 计算：3tan30°＋cos245°－2sin60°．18. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）．
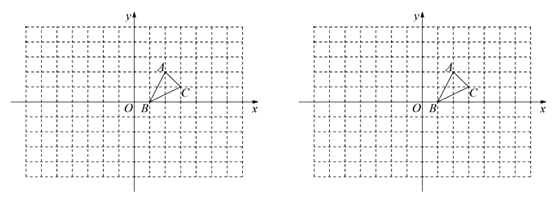(1)、在图1中画出△ABC关于y轴对称的△A1B1C1 ， 直接写出点C的对应点C1的坐标．
(2)、在图2中，以点O为位似中心，将△ABC放大，使放大后的△A2B2C2与△ABC的对应边的比为2：1（画出一种即可）．直接写出点C的对应点C2的坐标．
19. 如图，AB为⊙O的直径，弦CD⊥AB于点E，连接BC．若AB＝6，∠B＝30°，求弦CD的长．
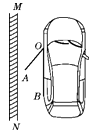
20. 如图所示是两张形状、大小相同但是画面不同的图片，把两张图片从中间剪断，再把四张形状相同的小图片（标注a、b、c、d）混合在一起，从四张图片中随机摸取一张，接着再随机摸取一张，则这两张小图片恰好合成一张完整图片的概率是多少？
21. 大城市病之一——停车难，主要表现在居住停车位不足，停车资源结构性失衡，中心城区供需差距大等等．如图是王老师的车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，已知小汽车车门宽AO为1.2米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？请说明理由．（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）
22. 抛物线y=ax+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
(1)、根据上表填空：①抛物线与x轴的交点坐标是和；
②抛物线经过点（－3，）；
(2)、试确定抛物线y=ax2+bx+c的解析式．23. 如图，在Rt△ABC中，∠C=90°，点D是BC边的中点，BD=2，tanB= ．
(1)、求AD和AB的长；
(2)、求sin∠BAD的值．
24. 如图，在△ABC中，AB=AC，以AB为直径作半圆O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．
(1)、求证：EF是⊙O的切线．(2)、如果⊙O的半径为5，sin∠ADE= ，求BF的长．25. 如图，在平面直角坐标系xOy中，函数 （x＜0）的图象与直线y=x+2交于点A（－3，m）．
(1)、求k，m的值；(2)、已知点P（a，b）是直线y=x上，位于第三象限的点，过点P作平行于x轴的直线，交直线y=x+2于点M，过点P作平行于y轴的直线，交函数 （x＜0）的图象于点N．①当a=－1时，判断线段PM与PN的数量关系，并说明理由；
②若PN≥PM结合函数的图象，直接写出b的取值范围．
26. 阅读下列材料：实验数据显示，一般成人喝250毫升低度白酒后，其血液中酒精含量（毫克/百毫升）随时间的增加逐步增高达到峰值，之后血液中酒精含量随时间的增加逐渐降低．
小带根据相关数据和学习函数的经验，对血液中酒精含量随时间变化的规律进行了探究，发现血液中酒精含量y是时间x的函数，其中y表示血液中酒精含量（毫克/百毫升），x表示饮酒后的时间（小时）．
下表记录了6小时内11个时间点血液中酒精含量y（毫克/百毫升）随饮酒后的时间x（小时）（x＞0）的变化情况．
下面是小带的探究过程，请补充完整：
(1)、如图，在平面直角坐标系xOy中，以上表中各对数值为坐标描点，图中已给出部分点，请你描出剩余的点，画出血液中酒精含量y随时间x变化的函数图象；
(2)、观察表中数据及图象可发现此函数图象在直线 两侧可以用不同的函数表达式表示，请你任选其中一部分写出表达式；
(3)、按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：30在家喝完250毫升低度白酒，第二天早上7：00能否驾车去上班？请说明理由．
27. 在平面直角坐标系xOy中，反比例函数 的图象经过点A（1，4），B（m，n）．
(1)、求反比例函数 的解析式；(2)、若二次函数 的图象经过点B，求代数式 的值；
(3)、若反比例函数 的图象与二次函数 的图象只有一个交点，且该交点在直线y＝x的下方，结合函数图象，求a的取值范围．28. 在平面直角坐标系xOy中，过⊙C上一点P作⊙C的切线l．当入射光线照射在点P处时，产生反射，且满足：反射光线与切线l的夹角和入射光线与切线l的夹角相等，点P称为反射点．规定：光线不能“穿过”⊙C，即当入射光线在⊙C外时，只在圆外进行反射；当入射光线在⊙C内时，只在圆内进行反射．特别地，圆的切线不能作为入射光线和反射光线．光线在⊙C外反射的示意图如图1所示，其中∠1=∠2．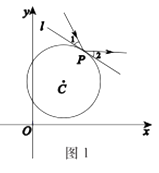
(1)、自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示，P1是第1个反射点．请在图2中作出光线经⊙C第二次反射后的反射光线和反射点P2；
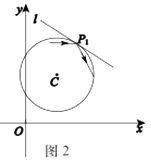(2)、当⊙O的半径为1时，如图3：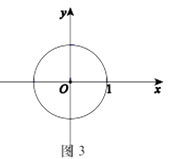
①第一象限内的一条入射光线平行于y轴，且自⊙O的外部照射在圆上点P处，此光线经⊙O反射后，反射光线与x轴平行，则反射光线与切线l的夹角为°；
②自点M（0，1）出发的入射光线，在⊙O内顺时针方向不断地反射．若第1个反射点是P1 ， 第二个反射点是P2 ， 以此类推，第8个反射点是P8恰好与点M重合，则第1个反射点P1的坐标为；
(3)、如图4，点M的坐标为（0，2），⊙M的半径为1．第一象限内自点O出发的入射光线经⊙M反射后，反射光线与坐标轴无公共点，求反射点P的纵坐标的取值范围．