北京市通州区2018届九年级上学期数学期末考试试卷
试卷更新日期:2018-03-06 类型:期末考试
一、单选题
-
1. 若反比例函数的图象经过点 ,则该反比例函数的表达式为( )
A、 B、 C、 D、2. 已知一个扇形的半径是1,圆心角是120°,则这个扇形的弧长是( )
A、 B、 C、 D、3. 如图:为了测量某棵树的高度,小刚用长为2m的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点,此时,竹竿与这一点距离6m,与树相距15m,那么这棵的高度为( )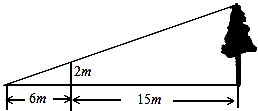 A、5米 B、7米 C、7.5米 D、21米4. 如图, 是⊙ 的直径,点 , 在⊙ 上.若 ,则 的度数为( )
A、5米 B、7米 C、7.5米 D、21米4. 如图, 是⊙ 的直径,点 , 在⊙ 上.若 ,则 的度数为( )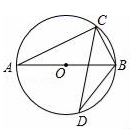 A、 B、 C、 D、5. 二次函数 的图象如图所示, ,则下列四个选项正确的是( )
A、 B、 C、 D、5. 二次函数 的图象如图所示, ,则下列四个选项正确的是( ) A、 , , B、 , , C、 , , D、 , ,6. 如图,⊙ 的半径为4.将⊙ 的一部分沿着弦 翻折,劣弧恰好经过圆心 .则折痕AB的长为( )
A、 , , B、 , , C、 , , D、 , ,6. 如图,⊙ 的半径为4.将⊙ 的一部分沿着弦 翻折,劣弧恰好经过圆心 .则折痕AB的长为( ) A、 B、 C、 D、7. 如图,在由边长为1的小正方形组成的网格中,点A,B,C都在小正方形的顶点上.则 的值为( )
A、 B、 C、 D、7. 如图,在由边长为1的小正方形组成的网格中,点A,B,C都在小正方形的顶点上.则 的值为( ) A、 B、 C、 D、8. 如图,在 中, , .点 为 边上一点,以每秒1单位的速度从点 出发,沿着 的路径运动到点 为止.连接 ,以点 为圆心, 长为半径作⊙ ,⊙ 与线段 交于点 .设扇形 面积为 ,点 的运动时间为 .则在以下四个函数图象中,最符合扇形面积 关于运动时间 的变化趋势的是( )
A、 B、 C、 D、8. 如图,在 中, , .点 为 边上一点,以每秒1单位的速度从点 出发,沿着 的路径运动到点 为止.连接 ,以点 为圆心, 长为半径作⊙ ,⊙ 与线段 交于点 .设扇形 面积为 ,点 的运动时间为 .则在以下四个函数图象中,最符合扇形面积 关于运动时间 的变化趋势的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 请你写出一个顶点在 轴上的二次函数表达式.
10. 已知点 , 在反比例函数 上,当 时, , 的大小关系是.
11. 如图,角 的一边在 轴上,另一边为射线 .则 . 12. 如图,点 为 的 边上一点, , .若 ,则 .
12. 如图,点 为 的 边上一点, , .若 ,则 . 13. 如图, , 是正六边形的两条对角线.在不添加任何其他线段的情况下,请写出两个关于图中角度的正确结论:
13. 如图, , 是正六边形的两条对角线.在不添加任何其他线段的情况下,请写出两个关于图中角度的正确结论: (1)、;(2)、.14. 二次函数 的部分图象如图所示,由图象可知,不等式 的解集为.
(1)、;(2)、.14. 二次函数 的部分图象如图所示,由图象可知,不等式 的解集为. 15. ⊙ 的半径为1,其内接 的边 ,则 的度数为.16. 阅读下面材料:
15. ⊙ 的半径为1,其内接 的边 ,则 的度数为.16. 阅读下面材料:在数学课上,老师提出如下问题:
尺规作图:作已知角的角平分线.
已知:如图,已知 .
求作: 的角平分线 .

小霞的作法如下:
①如图,在平面内任取一点 ;
②以点 为圆心, 为半径作圆,交射线 于点 ,交射线 于点 ;
③连接 ,过点 作射线 垂直线段 ,交⊙ 于点 ;
④连接 .

所以射线 为所求.
老师说:“小霞的作法正确.”
请回答:小霞的作图依据是 .
三、解答题
-
17. 计算: .
18. 如图,在平面直角坐标系 中,一次函数 与反比例函数 交于点 , .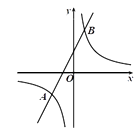 (1)、分别求出反比例函数和一次函数的表达式;(2)、根据函数图象,直接写出不等式 的解集.
(1)、分别求出反比例函数和一次函数的表达式;(2)、根据函数图象,直接写出不等式 的解集.
19. 如图, 内接于⊙ .若⊙ 的半径为6, ,求 的长. 20. 如图,建筑物的高 为17. 32米.在其楼顶 ,测得旗杆底部 的俯角 为 ,旗杆顶部 的仰角 为 ,请你计算旗杆的高度.( , , , ,结果精确到0.1米)
20. 如图,建筑物的高 为17. 32米.在其楼顶 ,测得旗杆底部 的俯角 为 ,旗杆顶部 的仰角 为 ,请你计算旗杆的高度.( , , , ,结果精确到0.1米) 21. 如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区 . 已知教学楼外墙长50米,设矩形 的边 米,面积为 平方米.
21. 如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区 . 已知教学楼外墙长50米,设矩形 的边 米,面积为 平方米. (1)、请写出活动区面积 与 之间的关系式,并指出 的取值范围;
(1)、请写出活动区面积 与 之间的关系式,并指出 的取值范围;
(2)、当 为多少米时,活动区的面积最大?最大面积是多少?22. 如图, 是等腰三角形, ,以 为直径的⊙ 与 交于点 , ,垂足为 , 的延长线与 的延长线交于点 . (1)、求证: 是⊙ 的切线;(2)、若⊙ 的半径为2, ,求 的值.
(1)、求证: 是⊙ 的切线;(2)、若⊙ 的半径为2, ,求 的值.
23. 如图1,在矩形 中,点 为 边中点,点 为 边中点;点 , 为 边三等分点, , 为 边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形 的面积与图3中四边形 的面积相等吗? (1)、小瑞的探究过程如下
(1)、小瑞的探究过程如下在图2中,小瑞发现, ;在图3中,小瑞对四边形 面积的探究如下. 请你将小瑞的思路填写完整:
设 ,
∵
∴ ,且相似比为 ,得到
∵
∴ ,且相似比为 ,得到
又∵ ,
∴
∴a= b, , b
∴ ,则 (填写“ ”,“ ”或“ ”)
(2)、小瑞又按照图4的方式连接矩形 对边上的点.则 24. 在平面直角坐标系 中,二次函数 的对称轴为 .点 在直线 上.
24. 在平面直角坐标系 中,二次函数 的对称轴为 .点 在直线 上. (1)、求 , 的值;(2)、若点 在二次函数 上,求 的值;
(1)、求 , 的值;(2)、若点 在二次函数 上,求 的值;
(3)、当二次函数 与直线 相交于两点时,设左侧的交点为 ,若 ,求 的取值范围.
25. 点 的“ 值”定义如下:若点 为圆上任意一点,线段 长度的最大值与最小值之差即为点 的“ 值”,记为 .特别的,当点 , 重合时,线段 的长度为0.当⊙ 的半径为2时:
 (1)、若点 , ,则 , ;
(1)、若点 , ,则 , ;
(2)、若在直线 上存在点 ,使得 ,求出点 的横坐标;
(3)、直线 与 轴, 轴分别交于点 , .若线段 上存在点 ,使得 ,请你直接写出 的取值范围.