北京市顺义区2018届九年级上学期数学期末考试试卷

试卷更新日期：2018-03-06 类型：期末考试

进入出卷网下载

一、单选题

1. 实数a，b，c，d在数轴上的对应点位置如图所示，这四个数中，绝对值最小的是（）

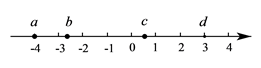A、a B、b C、c D、d

查看试题解析
2. 如图，在△ABC中，∠A=90°．若AB=12，AC=5，则cosC的值为（）

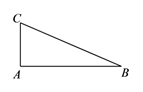A、 $\frac{5}{13}$ B、 $\frac{12}{13}$ C、 $\frac{5}{12}$ D、 $\frac{12}{5}$

查看试题解析
3. 下图是百度地图中截取的一部分，图中比例尺为1：60000，则卧龙公园到顺义地铁站的实际距离约为（）（注：比例尺等于图上距离与实际距离的比）

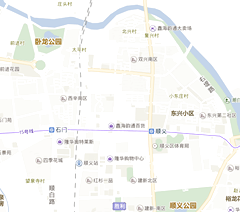A、1.5公里 B、1.8公里 C、15公里 D、18公里

查看试题解析
4. 已知蓄电池的电压为定值，使用蓄电池时，电流I(单位：A)与电阻R(单位：Ω)是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为（）

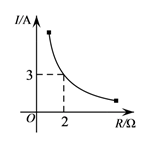A、 $I = \frac{3}{R}$ B、 $I = - \frac{6}{R}$ C、 $I = - \frac{3}{R}$ D、 $I = \frac{6}{R}$

查看试题解析
5. 二次函数的部分图象如图所示，对称轴是 $x = - 1$ ，则这个二次函数的表达式为（）

A、 $y = - x^{2} + 2 x + 3$ B、 $y = x^{2} + 2 x + 3$ C、 $y = - x^{2} + 2 x - 3$ D、 $y = - x^{2} - 2 x + 3$

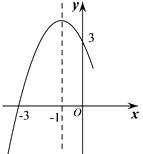查看试题解析
6. 如图，已知⊙O的半径为6，弦AB的长为8，则圆心O到AB的距离为（）

A、 $\sqrt{5}$ B、 $2 \sqrt{5}$ C、 $2 \sqrt{7}$ D、 $10$

查看试题解析
7. 已知△ABC，D，E分别在AB，AC边上，且DE∥BC，AD=2，DB=3，△ADE面积是4则四边形DBCE的面积是（）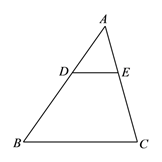

A、6 B、9 C、21 D、25

查看试题解析
8. 如图1，点P从△ABC 的顶点A出发，沿A-B-C匀速运动，到点C停止运动．点P 运动时，线段AP的长度 $y$ 与运动时间 $x$ 的函数关系如图2所示，其中D为曲线部分的最低点，则△ABC 的面积是（）

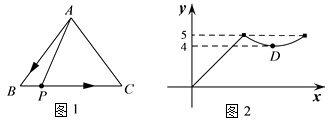A、10 B、12 C、20 D、24

查看试题解析

二、填空题

9. 分解因式：a²b﹣2ab+b= ．

查看试题解析
10. 如图，利用成直角的墙角（墙足够长），用10m长的栅栏围成一个矩形的小花园，花园的面积S（m²）与它一边长a（m）的函数关系式是，面积S的最大值是．

查看试题解析
11. 已知∠α，∠β如图所示，则tan∠α与tan∠β的大小关系是．

查看试题解析
12. 如图标记了 △ABC与△DEF边、角的一些数据，如果再添加一个条件使△ABC∽△DEF，那么这个条件可以是．（只填一个即可）

查看试题解析
13. 已知矩形ABCD中， AB=4，BC=3，以点B为圆心r为半径作圆，且⊙B与边CD有唯一公共点，则r的取值范围是．

查看试题解析
14. 已知y与x的函数满足下列条件：①它的图象经过（1，1）点；②当 $x > 1$ 时，y随x的增大而减小．写出一个符合条件的函数：．

查看试题解析
15. 在 $△ A B C$ 中， $∠ A = 45^{\circ}$ ， $A B = \sqrt{6}$ ， $B C = 2$ ，则AC的长为．

查看试题解析
16. 在平面直角坐标系xOy中，抛物线 $y_{1} = x^{2} + 2 x + 2$ 可以看作是抛物线 $y_{2} = - x^{2} - 2 x - 1$ 经过若干次图形的变化（平移、翻折、旋转）得到的，写出一种由抛物线y₂得到抛物线y₁的过程：．

查看试题解析

三、解答题

17. 解不等式组： ${\begin{matrix} 5 (x - 2) \leq 3 x + 6 \\ \frac{x - 5}{2} < 1 + 4 x \end{matrix}$ ．

查看试题解析
18. 计算： $| \sqrt{2} - 1 | + 2 sin 45 ° - \sqrt{8} + {tan}^{2} 60 °$ ．

查看试题解析
19. 如图，E是▱ABCD的边BC延长线上一点，AE交CD于点F，FG∥AD交AB于点G．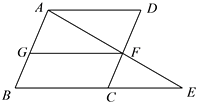

(1)、填空：图中与△CEF相似的三角形有；（写出图中与△CEF相似的所有三角形）

(2)、从（1）中选出一个三角形，并证明它与△CEF相似．

查看试题解析
20. 制造弯形管道时，经常要先按中心线计算“展直长度”，再备料．下图是一段管道，其中直管道部分AB的长为3 000mm，弯形管道部分BC，CD弧的半径都是1 000mm，∠O=∠O’=90°，计算图中中心虚线的长度．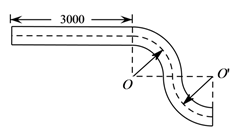

查看试题解析
21. 已知二次函数y=x²-4x+3．

(1)、在网格中，画出该函数的图象．

(2)、（1）中图象与 $x$ 轴的交点记为A，B，若该图象上存在一点C，且△ABC的面积为3，求点C的坐标．

查看试题解析
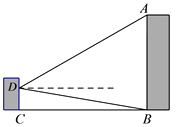
22. 已知：如图，在△ABC的中，AD是角平分线，E是AD上一点，且AB ：AC = AE ：AD．求证：BE=BD．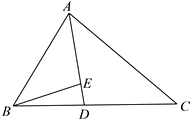

查看试题解析
23. 如图所示，某小组同学为了测量对面楼AB的高度，分工合作，有的组员测得两楼间距离为40米，有的组员在教室窗户处测得楼顶端A的仰角为30°，底端B的俯角为10°，请你根据以上数据，求出楼AB的高度．（精确到0.1米）
（参考数据：sin10°≈0.17， cos10°≈0.98， tan10°≈0.18， $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
24. 已知：如图， AB为⊙O的直径，CE⊥AB于E，BF∥OC，连接BC，CF．
求证：∠OCF=∠ECB．

查看试题解析
25. 如图，在平面直角坐标系xOy中，直线 $y = x - 2$ 与双曲线 $y = \frac{k}{x}$ （k≠0）相交于A，B 两点，且点A的横坐标是3．

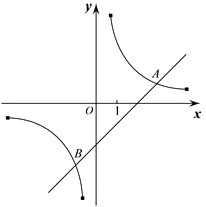(1)、求k的值；

(2)、过点P（0，n）作直线，使直线与x轴平行，直线与直线 $y = x - 2$ 交于点M，与双曲线 $y = \frac{k}{x}$ （k≠0）交于点N，若点M在N右边，求n的取值范围．

查看试题解析
26. 已知：如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作⊙O的切线交AB于点E，交AC的延长线于点F．

(1)、求证：DE⊥AB；

(2)、若tan∠BDE= $\frac{1}{2}$ ， CF=3，求DF的长．

查看试题解析
27. 综合实践课上，某小组同学将直角三角形纸片放到横线纸上（所有横线都平行，且相邻两条平行线的距离为1），使直角三角形纸片的顶点恰巧在横线上，发现这样能求出三角形的边长．

(1)、如图1，已知等腰直角三角形纸片△ABC，∠ACB=90°，AC=BC，同学们通过构造直角三角形的办法求出三角形三边的长，则AB=；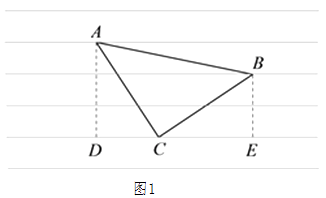

(2)、如图2，已知直角三角形纸片△DEF，∠DEF=90°，EF=2DE，求出DF的长；

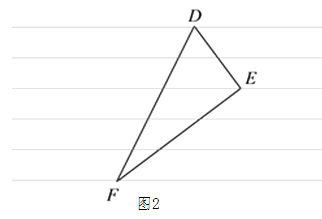(3)、在（2）的条件下，若橫格纸上过点E的横线与DF相交于点G，直接写出EG的长．

查看试题解析
28. 在平面直角坐标系xOy中，抛物线 $y = \frac{1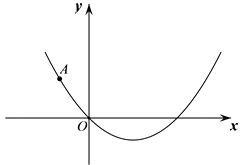}{9} x^{2} + b x$ 经过点A（-3，4）．

(1)、求b的值；

(2)、过点A作 $x$ 轴的平行线交抛物线于另一点B，在直线AB上任取一点P，作点A关于直线OP的对称点C；
①当点C恰巧落在 $x$ 轴时，求直线OP的表达式；
②连结BC，求BC的最小值．

查看试题解析