广东省深圳市南山区2017-2018学年七年级上学期数学期末考试试卷

试卷更新日期：2018-03-06 类型：期末考试

进入出卷网下载

一、选择题

1. 下列调查中，最适合采用普查方式进行的是（）

A、对深圳市居民日平均用水量的调查 B、对一批LED节能灯使用寿命的调查 C、对央视“新闻60分”栏目收视率的调查 D、对某中学教师的身体健康状况的调查

查看试题解析
2. 在下列日常生活的操作中，能体现基本事实“两点之间，线段最短”的是（）

A、用两颗钉子固定一根木条 B、把弯路改直可以缩短路程 C、用两根木桩拉一直线把树栽成一排 D、沿桌子的一边看，可将桌子排整齐

查看试题解析
3. 2017年11月19日上午8：00，“2017华润·深圳南山半程马拉松赛”在华润深圳湾体育中心(“春茧”)前正式开跑，共有约16000名选手参加了比赛.16000用科学记数法可表示为（）

A、0.16x10⁴ B、0.16x10⁵ C、1.6x10⁴ D、1.6x10⁵

查看试题解析
4. 下列计算正确的是（）

A、3x²y一2x²y=x^2y B、5y一3y=2 C、3a+2b=5ab D、7a+a=7a²

查看试题解析
5. 如图，已知线段AB=10cm，M是AB中点，点N在AB上，NB=2cm，那么线段MN的长为（）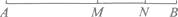

A、5cm B、4cm C、3cm D、2cm

查看试题解析
6. 下列结论中，正确的是（）

A、单项式 $\frac{3 x y^{2}_{^{}}}{7}$ 的系数是3，次数是2 B、单项式m的次数是1，没有系数 C、单项式-xy²z的系数是-1，次数是4 D、多项式2x²+xy+3是四次三项式

查看试题解析
7. 若x²+3x一5的值为7，则3x²+9x一2的值为（）

A、44 B、34 C、24 D、14

查看试题解析
8. 有理数a在数轴上的位置如图所示，下列各数中，可能在0到1之间的是（）

A、∣a∣-1 B、∣a∣ C、-a D、a+1

查看试题解析
9. 下图是小刚一天中的作息时间分配的扇形统计图，如果小刚希望把自己每天的阅读时间调整为2小时，那么他的阅读时间需增加（）

A、105分钟 B、60分钟 C、48分钟 D、15分钟

查看试题解析
10. 上图为一无盖长方体盒子的展开图(重叠部分不计)，可知该无盖长方体的容积为（）

A、4 B、6 C、12 D、8

查看试题解析
11. 某商场举办“迎新春送大礼”的促销活动，全场商品一律打八折销售．王老师买了一件商品，比标价少付了50元，那么他购买这件商品花了（）

A、250元 B、200元 C、150元 D、100元

查看试题解析
12. 如图所示，∠BAC=90°，AD⊥BC，则下列结论中，正确的个数为（   ）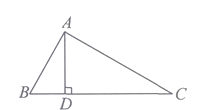

    ①AB⊥AC； ②AD与AC互相垂直； ③点C到AB的垂线段是线段AB；
    ④点A到BC的距离是线段AD的长度； ⑤线段AB的长度是点B到AC的距离；
    ⑥AD+BD>AB．

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 如图所示，截去正方体的一个角后变成了一个新的多面体，这个多面体有个面．

查看试题解析
14. a的相反数是一 $\frac{3}{2}$ ，则a的倒数是．

查看试题解析
15. x，y表示两个数，规定新运算“※”及“△”如下：x※y=6x+5y，x △ y=3xy，那么(一2※3) △(-4)= ．

查看试题解析
16. 如图都是由同样大小的黑棋子按一定规律摆出的图案，第①个图案有4个黑棋子，第②个图案有9个黑棋子，第③个图案有14个黑棋子，…，依此规律，第n个图案有1499个黑棋子，则n= ．

查看试题解析

三、解答题

17. 计算：

(1)、(-4)×3+(-18)÷(-2)

(2)、 $- 2^{2} + (\frac{2}{3} - \frac{3}{4}) \times 12$

(3)、先化简，再求值：x²一(5x²—4y)+3(x²一y)其中x=一1，y=2．

查看试题解析
18. 解答下列方程的问题

(1)、已知x=3是关于x的方程：4x—a=3+ax的解，那么a的值是多少?

(2)、解方程： $\frac{5 x - 7}{6} + 1 = \frac{3 x - 1}{4}$

查看试题解析
19. 如图1，是由一些棱长为单位1的相同的小正方体组合成的简单几何体．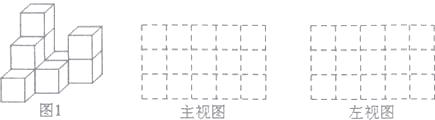

(1)、图中有个小正方体；

(2)、请在图1右侧方格中分别画出几何体的主视图、左视图；

(3)、不改变(2)中所画的主视图和左视图，最多还能在图1中添加个小正方体．

查看试题解析
20. 随着互联网的发展，同学们的学习习惯也有了改变，一些同学在做题遇到困难时，喜欢上网查找答案．针对这个问题，某校调查了部分学生对这种做法的意见(分为：赞成、无所谓、反对)，并将调查结果绘制成图1和图2两个不完整的统计图．
请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了多少名学生?

(2)、将图1补充完整；

(3)、求出扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数；

(4)、根据抽样调查结果，请你估计该校1500名学生中有多少名学生持“无所谓”意见．

查看试题解析
21. 我们已学习了角平分线的概念，那么你会用他们解决有关问题吗?

(1)、如图1所示，将长方形笔记本活页纸片的一角折过去，使角的顶点A落在A’处，BC为折痕．若∠ABC=54°，求∠A'BD的度数．

(2)、在(1)条件下，如果又将它的另一个角也斜折过去，并使BD边与BA’重合，折痕为BE，如图2所示，求∠CBE的度数．

查看试题解析
22. 阅读理解：高斯上小学时，有一次数学老师让同学们计算“从1到100这100个正整数的和”．许多同学都采用了依次累加的计算方法，计算起来非常烦琐，且易出错．聪明的小高斯经过探索后，给出了下面漂亮的解答过程．
解：设S=1+2+3+…+100， ①
则S=100+99+98+…+1，②
①+②，得
2S=101+101+101+…+101．
(两式左右两端分别相加，左端等于2s，右端等于100个101的和)
所以2S=100x101，
S= $\frac{1}{2}$ ×100x101=5050 ③
所以1+2+3+…+100=5050．
后来人们将小高斯的这种解答方法概括为“倒序相加法”．
请解答下面的问题：

(1)、请你运用高斯的“倒序相加法”计算：1+2+3+…+200．

(2)、请你认真观察上面解答过程中的③式及你运算过程中出现类似的③式，猜想：
1+2+3+…+n= ．

(3)、计算：101+102+103+…+2018．

查看试题解析
23. 以下是两张不同类型火车的车票(“Dxxxx次”表示动车，“GXXXX次”表示高铁)：

(1)、根据车票中的信息填空：该列动车和高铁是向而行(填“相”或“同”)．

(2)、已知该动车和高铁的平均速度分别为200km／h、300km／h，两列火车的车身长度不计．
①经过测算，如果两列火车直达终点(即中途都不停靠任何站点)，高铁比动车将早到1小时，求A、B两地之间的距离(温馨提醒：注意两张火车票的发车时间)．
②在①中测算的数据基础上，已知A、B两地途中依次设有5个站点P₁、P₂、P₃、P₄、P₅ ，且AP₁=P₁P₂=P₂P₃=P₃P₄=P₄P₅=P₅B，动车每个站点都停靠，高铁只停靠P₂、P₄两个站点，两列火车在每个停靠站点都停留5分钟．求该列高铁追上动车的时刻．

查看试题解析