广东省深圳市南山区2017-2018学年九年级上学期数学期末考试试卷
试卷更新日期:2018-03-06 类型:期末考试
一、选择题
-
1. 如图所示的工件,其俯视图是( )
 A、
A、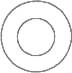 B、
B、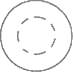 C、
C、 D、
D、 2. 当x<0时,函数y=- 的图象在( )
2. 当x<0时,函数y=- 的图象在( )
A、第四象限 B、第三象限 C、第二象限 D、第一象限3. 如果 , 那么下列等式中不一定成立的是( )
A、 B、 C、 D、ad=bc4. 矩形、菱形、正方形都一定具有的性质是( )A、邻边相等 B、四个角都是直角 C、对角线相等 D、对角线互相平分5. 下列说法正确的是( )
A、菱形都是相似图形 B、各边对应成比例的多边形是相似多边形 C、等边三角形都是相似三角形 D、矩形都是相似图形6. 某学校要种植一块面积为100m2的长方形草坪,要求两边长均不小于5m,则草坪的一边长为y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )A、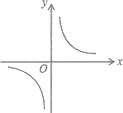 B、
B、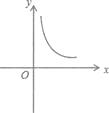 C、
C、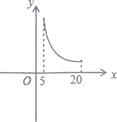 D、
D、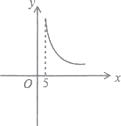 7. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程为( )
7. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1892张照片,如果全班有x名同学,根据题意,列出方程为( )
A、x(x+1)=1892 B、x(x-1)=1892x2 C、x(x-1)=1892 D、2x(x+1)=18928. 如图,△ABC中,DEBC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )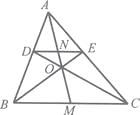 A、 B、 C、 D、9. 如图,菱形ABCD的周长为16,ABC=120°,则AC的长为( )
A、 B、 C、 D、9. 如图,菱形ABCD的周长为16,ABC=120°,则AC的长为( )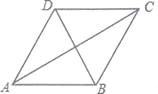 A、4 B、4 C、2 D、210. 已知:线段AB,BC,∠ABC=90。 . 求作:矩形ABCD.以下是甲、乙两同学的作业:
A、4 B、4 C、2 D、210. 已知:线段AB,BC,∠ABC=90。 . 求作:矩形ABCD.以下是甲、乙两同学的作业:
对于两人的作业,下列说法正确的是( )
A、两人都对 B、两人都不对 C、甲对,乙不对 D、甲不对,乙对11. 如图,在平面直角坐标系中,直线y1=2x-2与坐标轴交于A、B两点,与双曲线y2= (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论错误的是( )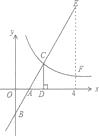
A、当x>0时,y1随x的增大而增大,y2随x的增大而减小; B、k=4: C、当0<x<2时,y1< y2 D、当x=4时,EF=4.12. 如图,已知在矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连接BD,过点E作EH⊥BD,垂足为H,连接口,交BD于点G,交BC于点旭连接CF.给出下列结论:①△CDE∽△CBF;②∠DBC=∠EFC;③ =;④GH的值为定值 ; 上述结论中正确的个数为( )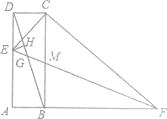 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 如图,是某射手在相同条件下进行射击训练的结果统计图,该射手击中靶心的概率的估计值为 .
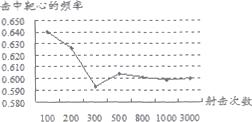 14. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则 = .
14. 如图,四边形ABCD与四边形EFGH位似,位似中心点是O, = ,则 = .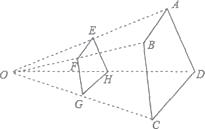 15. 已知点C是线段AB的黄金分割点,且AC>BC,AB=2,则AC .
15. 已知点C是线段AB的黄金分割点,且AC>BC,AB=2,则AC .
16. 如图,函数y=-x的图象与函数y= 的图象相交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,D.则四边形ACBD的面积为 .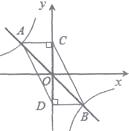
三、解答题
-
17. 解下列方程
(1)、x2+2x-1=0.
(2)、x(2x+3)=4x+6
18. 同学报名参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100m、200m、1000m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用T1、T2表示).(1)、该同学从5个项目中任选一个,恰好是田赛项目的概率P为;(2)、该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率P1为 , 利用列表法或树状图加以说明;
(3)、该同学从5个项目中任选两个,则两个项目都是径赛项目的概率P2为 .19. 如图,晚上小亮在广场上乘凉.图中线段AB表示站在广场上的小亮,线段P0表示直立在广场上的灯杆,点P表示照明灯.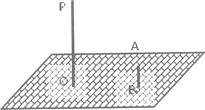 (1)、请你在图中画出小亮在照明灯P照射下的影子BC;
(1)、请你在图中画出小亮在照明灯P照射下的影子BC;
(2)、如果灯杆高PO=-12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.
20. 苏宁电器销售某种冰箱,每台的进货价为2600元,调查发现,当销售价为3000元时,平均每天能售出8台;而当销售价每降低100元时,平均每天就能多售出8台. 商场要使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
21. 如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90。得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.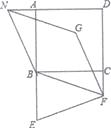 (1)、求证:BE=2CF;(2)、试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.22. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE= c,这时我们把关于x的形如ax2+ +b=0的一元二次方程称为“勾系一元二次方程”.
(1)、求证:BE=2CF;(2)、试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.22. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE= c,这时我们把关于x的形如ax2+ +b=0的一元二次方程称为“勾系一元二次方程”.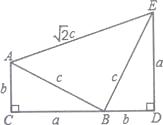
请解决下列问题:
(1)、写出一个“勾系一元二次方程”;
(2)、求证:关于x的“勾系一元二次方程”ax2+ +b=0必有实数根;
(3)、若x=-1是“勾系一元二次方程”ax2+ +b=0的一个根,且四边形ACDE的周长是6 ,求△ABC面积.
23. 如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折现”)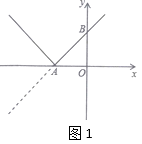 (1)、类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;(2)、如图2,双曲线y= 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
(1)、类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;(2)、如图2,双曲线y= 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.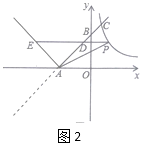
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.