2017-2018学年北师大版数学八年级下册同步训练：1.2 直角三角形 课时2
试卷更新日期：2018-03-05 类型：同步测试
一、填空题
-
1. 如图，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D，下面四个结论：①∠ABE=∠BAD；②△CEB≌△ADC；③AB=CE；④AD-BE=DE.其中正确的是 (将你认为正确结论的序号都写上).
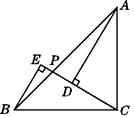
2. 如图，MN∥PQ，AB⊥PQ，点A，D在直线MN上，点B，C在直线PQ上，点E在AB上，AD+BC=7，AD=EB，DE=EC，则AB=
3. 判定三角形全等的方法有4种，分别是 ， ， ， ；判定直角三角形全等的方法有5种，分别是 ， ， ， ， 。
二、选择题
-
4. 如图，∠B=∠D=90°，AB=AD，则能够说明△ABC≌△ADC的理由是（ ）
A、ASA B、AAS C、SAS D、HL5. 如图，∠C=∠D=90°，添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是（ ）
A、AC=AD B、AB=AB C、∠ABC=∠ABD D、∠BAC=∠BAD6. 如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C，D，则下列结论错误的是（ ）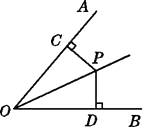
A、PC=PD B、∠CPO=∠DOP C、∠CPO=∠DPO D、OC=OD7. 如图，在△ABC中，∠C=90°，ED⊥AB于点D，BD=BC，若AC=6 cm，则AE+DE等于（ ）
A、4 cm B、5 cm C、6 cm D、7 cm8. 如图，在△ABC中，AD⊥BC，D为BC的中点，以下结论：①△ABD≌△ACD；②AB=AC；③∠B=∠C；④AD是△ABC的角平分线.其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个9. 如图，H是△ABC的高AD，BE的交点，且DH=DC，则下列结论：①BD=AD；②BC=AC；③BH=AC；④CE=CD中，正确的有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，下列条件不能证明△ABD≌△ACD的是（ ）
A、BD=DC，AB=AC B、∠ADB=∠ADC，BD=DC C、∠B=∠C，∠BAD=∠CAD D、∠B=∠C，BD=DC11. 在Rt△ABC和Rt△A'B'C'中，∠C=∠C'=90°，下列条件中，能判定Rt△ABC≌Rt△A'B'C'的个数为（ ）①AC=A'B'，∠A=∠A'；②AC=A'C'，AB=A'B'；
③AC=A'C'，BC=B'C'； ④AB=A'B'，∠A=∠A'.
A、1 B、2 C、3 D、412. 如图，已知∠E=∠F=90°，∠B=∠C，AE=AF，下列结论：①EM=FN；②CD=DN；③∠FAN=∠EAM；④△ACN≌△ABM.其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个13. 如图，AB∥DE，AC∥DF，AC=DF，下列条件中，不能判断△ABC≌△DEF的是（ ）
A、AB=DE B、∠B=∠E C、EF=BC D、EF∥BC三、解答题
-
14. 如图，D是△ABC的边BC的中点，DE⊥AC，DF⊥AB，垂足分别为E，F，且BF=CE.求证：∠B=∠C.
