2017-2018学年北师大版数学八年级下册同步训练：1.1 等腰三角形 课时4
试卷更新日期：2018-03-05 类型：同步测试
一、填空题
-
1. 三个角都的三角形是等边三角形;有一个角是的等腰三角形是等边三角形.2. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于
二、选择题
-
3. 等腰三角形补充下列条件后，仍不一定成为等边三角形的是（ ）A、有一个内角是60° B、有一个外角是120° C、有两个角相等 D、腰与底边相等4. 下列三角形：
①有两个角等于60°的三角形；
②有一个角等于60°的等腰三角形；
③三个外角(每个顶点处各取一个外角)都相等的三角形；
④一腰上的中线也是这条腰上的高的等腰三角形.
其中是等边三角形的有（ ）
A、①②③ B、①②④ C、①③ D、①②③④5. 如图，木工师傅从边长为90 cm的正三角形木板上锯出一个正六边形木板，那么正六边形木板的边长为（ ）
A、34 cm B、32 cm C、30 cm D、28 cm6. 如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面的结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（ ）
A、1个 B、2个 C、3个 D、4个7. 如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（ ）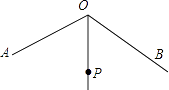
A、1个 B、2个 C、3个 D、3个以上8. 如图，在△ABC中，∠C=90°，∠A=30°，AB=12，则BC等于（ ）
A、6 B、6 C、6 D、129. 在△ABC中，∠A∶∠B∶∠C=1∶2∶3，则BC∶AB等于（ ）A、2∶1 B、1∶2 C、1∶3 D、2∶310. 如图，在△ABC中，∠C=90°，AC=3，∠B=30°，点P是线段BC边上的动点，则AP长不可能是（ ）
A、3.5 B、4.2 C、5.8 D、711. 如图，在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线DE交AB于点E，交BC于点D，CD=3，则BC的长为（ ）
A、6 B、6 C、9 D、312. 如图，在△ABC中，∠ACB=90°，∠B=15°，DE垂直平分AB，交BC于点E，垂足为D，若BE=6 cm，则AC等于（ ）
A、6cm B、5cm C、4cm D、3cm13. 如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB，CD分别表示一楼、二楼地面的水平线，∠ABC=150°，BC的长是8 m，则乘电梯从点B到点C上升的高度h是（ ）
A、3m B、4m C、5m D、6m14. 如图，一棵大树在一次强台风中从离地面5 m处折断倒下，倒下部分与地面成30°角，这棵大树在折断前的高度为（ ）
A、10m B、15m C、25m D、30m三、解答题
-
15. 如图，在△ABC中，∠ACB=120°，CD平分∠ACB，AE∥DC，交BC的延长线于点E.
求证：△ACE是等边三角形.
