2017-2018学年北师大版数学八年级下册同步训练：1.1 等腰三角形 课时3
试卷更新日期：2018-03-05 类型：同步测试
一、填空题
-
1. 如果一个三角形有两个角相等,那么这两个角所对的边也 ， 简称:“等角对”
2. 反证法：先假设命题的不成立，然后推导出与定义、基本事实、已有定理或已知条件相的结果，从而证明命题的结论成立，这种证明方法称为反证法.
二、选择题
-
3. 如图，在△ABC中，∠B=∠C，AB=5，则AC的长为（ ）
A、2 B、3 C、4 D、54. 在△ABC中，∠A和∠B的度数如下，能判定△ABC是等腰三角形的是（ ）
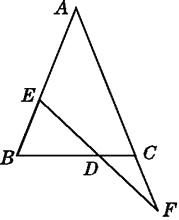
A、∠A=50°，∠B=70° B、∠A=70°，∠B=40° C、∠A=30°，∠B=90° D、∠A=80°，∠B=60°5. 如图，∠B=∠C=36°，∠ADE=∠AED=72°，则图中的等腰三角形有（ ）
A、3个 B、4个 C、5个 D、6个6. 如图，在△ABC中，AB=AC，DE∥BC，则下列结论中不正确的是（ ）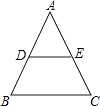
A、AD=AE B、DB=EC C、∠ADE=∠C D、DE= BC7. 如图，在△ABC中，∠A=36°，AB=AC，BD是△ABC的角平分线．若在边AB上截取BE=BC，连接DE，则图中等腰三角形共有（ ）
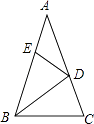A、2个 B、3个 C、4个 D、5个8. 在△ABC中，∠A∶∠B∶∠C=1∶1∶2，则△ABC是（ ）
A、等腰三角形 B、直角三角形 C、锐角三角形 D、等腰直角三角形9. 如图，AD是△ABC的边BC上的高，添加下列条件中的某一个，不能推出△ABC为等腰三角形的是（ ）
A、∠BAD=∠ACD B、∠BAD=∠CAD C、BD=CD D、∠B=∠C10. 如图所示的正方形网格中，网格线的交点称为格点，已知A，B是两格点，若C也是格点，且使得△ABC为等腰三角形，则点C的个数是（ ）
A、6 B、7 C、8 D、911. 如图，在△ABC中，AB=20cm，AC=12 cm，点P从点B出发以每秒3 cm的速度向点A运动，点Q从点A同时出发以每秒2 cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当∠APQ=∠AQP时，P，Q运动的时间为（ ）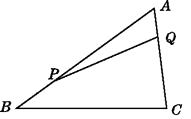
A、3秒 B、4秒 C、4.5秒 D、5秒12. “a<b”的反面应是（ ）
A、a>b且a≠b B、a>b C、a=b D、a=b或a>b13. 用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”时，应先假设（ ）A、有一个锐角小于45° B、每一个锐角都小于45° C、有一个锐角大于45° D、每一个锐角都大于45°14. 下列命题中，宜用反证法证明的是（ ）A、等腰三角形两腰上的高相等 B、有一个外角是120°的等腰三角形是等边三角形 C、两条直线都与第三条直线平行，则这两条直线互相平行 D、全等三角形的面积相等三、解答题
