2017-2018学年北师大版数学九年级下册同步训练：1.4 解直角三角形

试卷更新日期：2018-03-05 类型：同步测试

进入出卷网下载

一、选择题

1. 在△ABC中，∠C=90°，BC=4， $\sin A = \frac{2}{3}$ ，则边AC的长是（）

A、 $2 \sqrt{5}$ B、6 C、 $\frac{8}{3}$ D、 $2 \sqrt{13}$

查看试题解析
2.
如图，在△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC= $\frac{3}{5}$ ，则BC的长是（　　）

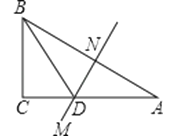A、4cm B、6cm C、8cm D、10cm

查看试题解析
3. 如图，已知AD是等腰△ABC底边BC上的高，sinB= $\frac{4}{5}$ ，点E在AC上，且AE：EC=2：3，则tan∠ADE=（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{2}{5}$

查看试题解析
4. 如何求tan75°的值？按下列方法作图可解决问题，如图，在Rt△ABC中，AC=k，∠ACB=90°，∠ABC=30°，延长CB至点M，在射线BM上截取线段BD，使BD=AB，连接AD，依据此图可求得tan75°的值为（）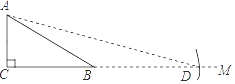

A、2 $- \sqrt{3}$ B、2+ $\sqrt{3}$ C、1+ $\sqrt{3}$ D、 $\sqrt{3} - 1$

查看试题解析
5. 已知在△ABC中，AB=14，BC=13，tanB= $\frac{12}{5}$ ，则sinA的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{7}{25}$ D、 $\frac{56}{65}$

查看试题解析
6. 设a、b、c分别为△ABC中∠A，∠B和∠C的对边，则△ABC的面积为（）

A、 $\frac{1}{2} a b \sin A$ B、 $\frac{1}{2} a b \sin B$ C、 $\frac{1}{2} a b \sin C$ D、 $\frac{1}{2} a b \cos C$

查看试题解析
7. 在△ABC中，∠C=90°，tanA= $\frac{12}{5}$ ，△ABC的周长为60，那么△ABC的面积为（）

A、60 B、30 C、240 D、120

查看试题解析
8. 如图，在等腰Rt△ABC中，∠C=90°，AC=BC=6，D是AC上一点，若tan∠DBA= $\frac{1}{5}$ ，则AD的长为（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{2}$ D、1

查看试题解析
9. 如图，△ABC中AB=AC=4，∠C=72°，D是AB中点，点E在AC上，DE⊥AB，则cosA的值为（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} - 1}{4}$ C、 $\frac{\sqrt{5} + 1}{4}$ D、 $\frac{\sqrt{5} + 1}{2}$

查看试题解析
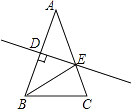10. 如图，在△ABC中，∠B=90°，tan∠C= $\frac{3}{4}$ ，AB=6cm．动点P从点A开始沿边AB向点B以1cm/s的速度移动，动点Q从点B开始沿边BC向点C以2cm/s的速度移动．若P，Q两点分别从A，B两点同时出发，在运动过程中，△PBQ的最大面积是（）

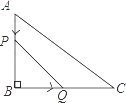A、18cm² B、12cm² C、9cm² D、3cm²

查看试题解析

二、填空题

11. △ABC中，AB=12，AC= $\sqrt{39}$ ，∠B=30°，则△ABC的面积是．

查看试题解析
12. 如图，在Rt△ABC中，∠ACB=90°，sinB= $\frac{3}{5}$ ，D是BC上一点，DE⊥AB于E，CD=DE，AC+CD=9．则BC= ．

查看试题解析
13. 如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”，在Rt△ABC中，∠C=90°，若Rt△ABC是“好玩三角形”，则tanA= ．

查看试题解析
14. 如图所示，四边形ABCD中，∠B=90°，AB=2，CD=8，AC⊥CD，若sin∠ACB= 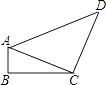$\frac{1}{3}$ ，则cos∠ADC= ．

查看试题解析
15. 如图，AD⊥CD，∠ABD=60°，AB=4m，∠ACB=45°，则AC= ．

查看试题解析
16. 已知：如图，在△ABC中，∠BAC=90°，点D在AB上，点E在CA的延长线上，连接DC、DE，∠EDC=45°，BD=EC，DE=5 $\sqrt{2}$ ，tan∠DCE= $\frac{3}{13}$ ，则CE= ．

查看试题解析

三、解答题

17. 某游乐场部分平面图如图所示，C、E、A在同一直线上，D、E、B在同一直线上，测得A处与E处的距离为80 米，C处与D处的距离为34米，∠C=90°，∠ABE=90°，∠BAE=30°．（ $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7）

(1)、求旋转木马E处到出口B处的距离；

(2)、求海洋球D处到出口B处的距离（结果保留整数）．

查看试题解析
18. 如图，△ABC中，∠ACB=90°，sinA= $\frac{4}{5}$ ，BC=8，D是AB中点，过点B作直线CD的垂线，垂足为点E．

(1)、求线段CD的长；

(2)、求cos∠ABE的值．

查看试题解析