2017-2018学年北师大版数学七年级下册同步训练：1.4 整式的乘法
试卷更新日期：2018-03-05 类型：同步测试
一、单选题
-
1. 若（x+2）（x﹣1）=x2+mx+n，则m+n=（ ）A、1 B、﹣2 C、﹣1 D、22. 下列计算正确的是（ ）A、x•2x=2x B、x3•x2=x5 C、（x2）3=x5 D、（2x）2=2x23. 单项式乘以多项式运算法则的依据是（ ）A、乘法交换律 B、加法结合律 C、乘法分配律 D、加法交换律4. 如（x+a）与（x+3）的乘积中不含x的一次项，则a的值为（ ）A、3 B、﹣3 C、1 D、﹣15. 李老师做了个长方形教具，其中一边长为2a+b，另一边长为a﹣b，则该长方形的面积为（ ）A、6a+b B、2a2﹣ab﹣b2 C、3a D、10a﹣b6. 若将代数式中的任意两个字母交换，代数式不变，则称这个代数式为完全对称式，如a+b+c就是完全对称式．下列三个代数式：
①（a﹣b）2；
②（2a﹣b）（2a+b）；
③a（a+b）．
其中是完全对称式的是（ ）
A、③ B、①③ C、②③ D、①7.如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式： ①（2a+b）（m+n）； ②2a（m+n）+b（m+n）；
③m（2a+b）+n（2a+b）； ④2am+2an+bm+bn，你认为其中正确的有（ ）
A、①② B、③④ C、①②③ D、①②③④8. 如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（a+3b），宽为（2a+b）的大长方形，则需要A类、B类和C类卡片的张数分别为（ ）
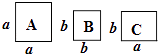A、2，3，7 B、3，7，2 C、2，5，3 D、2，5，7二、填空题
-
9. 已知m﹣n=2，mn=﹣1，则（1+2m）（1﹣2n）的值为 ．10. 若（1+x）（2x2+mx+5）的计算结果中x2项的系数为﹣3，则m=11. 若（2x+5）（4x﹣10）=8x2+px+q，则p= ， q= ．12. 光的速度每秒约3×105千米，太阳光射到地球上需要的时间约是5×102秒，则地球与太阳的距离约是千米．13. 如果单项式﹣3x4a﹣by2与 x3ya+b是同类项，那么这两个单项式的积是 ．14. 一个矩形的面积为（6ab2+4a2b）cm2 ， 一边长为2abcm，则它的周长为 cm．15. 对于实数a，b，c，d，规定一种运算 =ad﹣bc，如 =1×（﹣2）﹣0×2=﹣2，那么当 =27时，则x= ．
三、解答题
-
16. 先化简，再求值：2（x﹣3）（x+2）﹣（3+a）（3﹣a），其中a=﹣2，x=1．17. 已知一个多项式除以a2﹣3a+1得到商式是2a+1，求这个多项式．18. 若3x2﹣2x+b与x2+bx﹣1的和中不存在含x的项，试求b的值，写出它们的和，并证明不论x取什么值，它的值总是正数．19. 甲、乙两人共同计算一道整式乘法：（2x+a）（3x+b），由于甲抄错了第一个多项式中a前面的符号，得到的结果为6x2+18x+12；由于乙漏抄了第二个多项中的x的系数，得到的结果为2x2+2x﹣12，请你计算出a、b的值各是多少，并写出这道整式乘法的正确结果．20.
当我们利用2种不同的方法计算同一图形的面积时，可以得到一个等式．例如，由图1，可得等式：（a+2b）（a+b）=a2+3ab+2b2 ．
(1)、由图2，可得等式： ．(2)、利用（1）中所得到的结论，解决下面的问题：已知 a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；
(3)、利用图3中的纸片（足够多），画出一种拼图，使该拼图可用来验证等式：2a2+5ab+2b2=（2a+b）（a+2b）；(4)、小明用2 张边长为a 的正方形，3 张边长为b的正方形，5 张边长分别为a、b 的长方形纸片重新拼出一个长方形，那么该长方形较长的一条边长为 ．